7-6-4
My solution to the 7-6-4 acron was generated by following a similar set of rules to those used by Mason Green in his discovery of the 7-7-3 acrohedron. These are described here.
Starting with a virtual heptagon (i.e. a heptagon which is removed from the final polyhedron), surround it with a double ring of squares and hexagons. A ring of heptagons can be fitted to the exposed top edges of the squares and the exposed lateral edges of the hexagons. A second ring of squares can now be used to connect the exposed top edges of the hexagons and the adjacent exposed edges of the heptagons. (Part model here). The remaining exposed edges would now fit a second ring of hexagons. If these were to be inserted though they would overlap (here). Hexagons though can be 'creased' across a vertex to vertex diagonal. The two 'half-hexagons' that result can be thought of as being made up of two sets of three coplanar triangles. This creasing operation can be performed on the second ring of hexagons such that the exposed lateral edges co-incide and the top edges form a heptagram. The resulting figure is shown in the left hand image above. It has 70 faces ... and a genus of 1.
The coplanar faces can be resolved by replacing the central triangle in each half-hexagon with a tetrahedron. This has been done (with all the tetrahedra pointing inwards) on the right hand image above. The figure now has 85 faces ... and remains genus 1.
 Aplanar triangles (tetrahedra inverted): VRML, OFF |
 Aplanar triangles (tetrahedra everted): VRML, OFF |
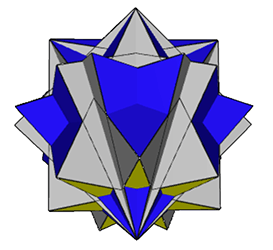
The above isomorph to the
7-6-4
contains 7/2-6-4 vertices. The heptagons in the 7-6-4 acrohedron
are
replaced by 7/2 heptagrams, and the 7/2-heptagram is replaced by a 7/3
heptagram. The same co-planarity problems exist as in the 7-6-4
acrohedron, the two minimal isomers exhibiting co-planar triangles are
shown top
right and top left. Again the co-planarity can be resolved by the
addition
of 14 tetrahedra, these have been placed pointing inwards in the lower
left
image (allowing the external structure to dominate) and outwards in the
lower
right image (allowing the internal structure to dominate. My
thanks to Roger
Kaufman for alerting me to the probable existence of this
isomorphs.
 OFF |
 OFF |
The 7-6-4 can be regarded as
an expanded version of the 7-7-3. Starting with the 7-7-3, move
the heptagonal faces apart until they are separated by a distance equal
to their edge length. Insert squares into these locations.
The triangular faces are replaced by hexagons.
The heptagonal faces can also
be moved inwards by a similar amount such that the squares can again be
inserted but the vertices are now crossed. The base {7} becomes a
{7/2} and the apex {7/2} becomes a single point. The result is
though degenerate as some of the vertices co-incide in pairs around the
equatorial heptagon. In similar fashion to the above, a 'great'
version exists which is also degenerate in the same way.