Pentakis
Rotundae
This
family
of polyhedra can be generated by taking a pentagonal
rotunda, and augmenting the lateral pentagonal faces with
pyramids. The triangular complexes have the flexibility to allow
n-gonal variants to be generated for values of n other than the
original pentagon. As with the rotunda and the cupolae, the
opposite polygon will be a 2n-gon. The family can also be
generated from the truncated tetrahedron
by replacing three of the hexagonal faceds with complexes of 6 coplanar
triangles.
Star
polyhedra
of the form {n/d} can also be used as the capping polygon. If d
is even then an family of semi-rotundae, similar in nature to the semicupolae can be
generated with a virtual {2n/d} base.
I have
concentrated my examples to date around n=7, although an example for n=9 has also been
generated. This is the upper limit for this family for convex
polygons, a regular
form for n=11 cannot be generated as the distance between the {11} and
{22} faces is too great to be spanned by the lateral faces.
In the images
and linked files below, the blue triangles are those present in the
original rotunda, the green triangles are those from the pentagonal
prisms.
Pentakis
Rotundae
|
Pentakis
Semi-Rotundae
|
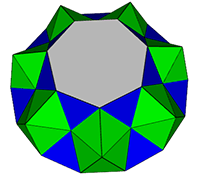
n=7
|
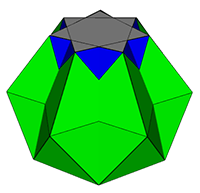
n=7/2 (virtual {7})
|
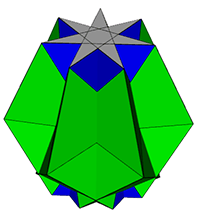
n=7/3
|
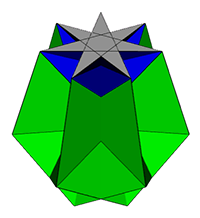
n=7/4 (virtual {7/2})
|
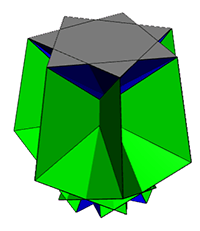
n=7/5
|
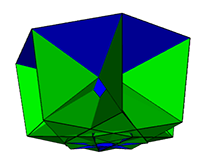
n=7/6 (virtual {7/3})
|
A variant
can also be generated with the pyramids facing inwards (example for n=7)
These polyhedra were generated using Great Stella, Antiprism and HEDRON.











