Monorhombal Edge Rhombified Polyhedra

This class of polyhedra is generated by replacing each edge of the original polyhedron by a rhombus. This breaks the planarity of the original faces, which is then addressed by replacing each of the original faces with a compound of triangles surrounding a central polygon. The resulting figure is then relaxed so that all edge lengths are equal. All faces other than the rhombi are then regular polygons. Emphasis is then placed on finding examples where the rhombi are alike, i.e. face-transient. A fuller term for these could then be 'monorhombal edge rhombified polyhedra'.

1. Isotoxal Uniform Polyhedra

If the process is successfully applied to an edge-transient (or 'isotoxal') uniform polyhedron, the resulting polyhedron automatically has all the rhombi face-transient. The process has been successfully applied to a number of the Platonic, Kepler-Pionsot and quasiregular uniform polyhedra (including the ditrigonals). However in the case of the deltahedra the resulting figure is always degenerate as the complex of four triangles on each original face is already regular and the rhombi relax to a width of zero. The hemihedra also do not appear to permit this process.

There appears to be only one solution per source polyhedron. In some cases the distortion from the original polyhedron is quite pronounced. In the table below, the images link to the edge rhombified polyhedra, the names underneath to the original uniform polyhedra.

E.R. Cube See Note 1	E.R. Dodecahedron See Notes 1 2 and 3
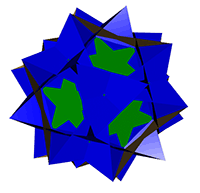
E.R. Great Icosidodecahedron ('gid')	E.R. Small Stellated Dodecahedron ('sissid')
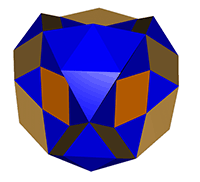
E.R.Great Stellated Dodecahedron ('gissid'). See Notes 2 and 4.	E.R.Cuboctahedron
E.R. Icosidodecahedron See Notes 2 and 5	E.R. Dodecadodecahedron
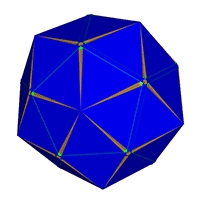
E.R.Great Dodecahedron ('gad')	E.R.Ditrigonal Dodecadodecahedron ('ditdid')
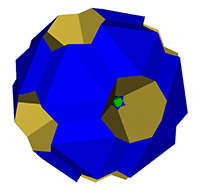
E.R.Small Ditrigonal Icosidodecahedron ('sidtid')	E.R.Great Ditrigonal Icosidodecahedron ('gidtid')

Notes:
1. Only the cube and dodecahedron produce convex monorhombal edge-rhombified polyhedra.
2. The rhombi in these polyhedra have an acute angle of acos(0.6), i.e. the same angle as is present in the Pythagorean 3-4-5 triangle.
3. This polyhedron is closely related to the rhombic enneacontahedron. Stellate it by adding pyramids over the pentagons such that the adjacent triangular faces become quadrilaterals, and then relax it such that they become rhombi.
4. The E.R.gissid required retrograde rhombi before it would relax, this is the only such case. The rhombi are otherwise the same shape as the edge-rhombified dodecahedron.
5. The relaxed rhombi have an acute angle of 72 degrees. The resulting figure is made of sections of icosidodecahedra and icosahedra connected by these rhombi.

2. Other Polyhedra

The duals of the semi-regular polyhedra, i.e. the rhombil dodecahedron and the three rhombic triacontahedra are also isotoxal. Given there are two distinct sets of vertices in each of these, it was not clear in advance that the rhombi would relax successfully but they did so with each of the original rhombic faces replaced by a complex of a square and four triangles.

E.R. Rhombic Dodecahedron	E.R. Rhombic Triacontahedron
E.R. Great Rhombic Triacontahedron	E.R. Medial Rhombic Triacontahedron

Further Resources

3D models of all the figures on this page are available here. This file contains VRML (*.wrl), *.OFF, Stella (*.stel) and HEDRON input (*.txt) files.

Credits

This paper was made possible using Robert Webb's excellent Great Stella program (www.software3d.com). Thanks are due to Roger Kaufman for his VRML2OFF utility, and to Scott Vorthmann for his VRML Revival project.

All VRML files were generated using Great Stella and post-processed with VRML2OFF and HEDRON.