Rectangular and Crossed-Rectangular Faced Polyhedra



Rectangular Faced Polyhedra

 R-R30


An isohedral polyhedra is one which is transitive on all faces.  Between 1998 and 2001 Coxeter  and Grunbaum ([1] and [2]) described four isohedral polyhedra where the faces are rectangular.  One of these had previously appeared in Bruckner 1900 [3] (see above), which he had found while exploring the duals to the stellations of the cuboctahedron.   Each of the rectangular isohedra can be created from the dual of a quasiregular polyhedron by replacing each pair of parallel rhombi with a ‘tube’ of four rectangles. 
 
The rectangles can be difficult to see in the completed polyhedron, particularly in the more complex examples, so links are provided below to each polyhedron with (a) one face hightlighted and (b) a 'tube' of four rectangular faces highlighted (as in the above example of the rectangulated rhombic triacontahedron).

Rectangular rhombic dodecahedron
One highlighted face
Four highlighted faces
Rectangular rhombic triacontahedron
One highlighted face
Four highlighted faces

Rectangular great rhombic triacontahedron
One highlighted face
Four highlighted faces
Rectangular medial rhombic triacontahedron
One highlighted face
Four highlighted faces

Crossed-Rectangular Faced Polyhedra


An extension of the above would be to consider isohedral polyhedra with ‘crossed rectangular’ faces. Such a face retains two parallel edges of the containing rectangle, with the other two edges being replaced by the diagonals of said rectangle.

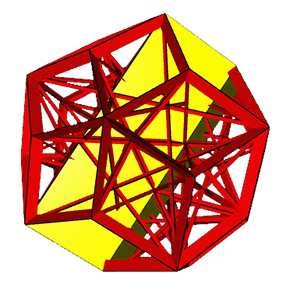
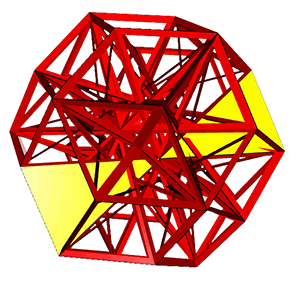
Using Great Stella, I was able to examine the facetings of the aforementioned duals and identify those meeting my criteria.  A total of twelve crossed-rectangular isohedra were produced.  The rhombic dodecahedron and medial rhombic tricontahedron produced two each, the rhombic triacontahedron and great rhombic triacontahedron produced four each.

Eight of the new polyhedra can be obtained by faceting the faces of the rectangular polyhedra with each rectangular polyhedron giving rise to two crossed-rectangular polyhedra.  In each case the rectangular face is replaced by a crossed-rectangular face sharing the same vertices.   These are suffixed ‘a’ and ‘b’ in the list below.  The ‘a’ case has the external edges of the rectangular polyhedron retained, the ‘b’ case has the internal edges retained.  It should be noted that the 'a' form for the crossed-rectangular rhombic dodecahedron is actually a compound of two polyhedra.  Both a single polyhedron and the compound are lined below.

In the case of the rhombic triacontahedron and the great rhombic triacontahedron, two further cases can be generated, suffixed ‘c’ and ‘d’.  The faces of these are unrelated to the rectangular polyhedra or to each other.  In all cases replacing the crossed-rectangular face with a rectangle or with the complimentary crossed-rectangle does not result in a valid polyhedron.

Again the crossed-rectangles can be difficult to see in the completed polyhedron, so links are provided below to each polyhedron with one face hightlighted.  The crossed rectangles do not form the 'tubes' as in the rectangular polyhedra.

For brevity, the term 'Crossed Rectangular' is shortened to 'XR' in the table below.
Crossed-Rectangular Rhombic Dodecahedra

XR rhombic dodecahedron (a)
One highlighted face
Compound
XR rhombic dodecahedron (b)
One highlighted face

Crossed-Rectangular Rhombic Triacontahedra

XR rhombic triacontahedron (a)
One highlighted face
XR rhombic triacontahedron (b)
One highlighted face

XR rhombic triacontahedron (c)
One highlighted face
XR rhombic triacontahedron (d)
One highlighted face
Crossed-Rectangular Great Rhombic Triacontahedra

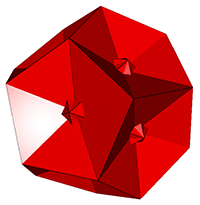
XR great rhombic dodecahedron (a)
One highlighted face
XR great rhombic dodecahedron (b)
One highlighted face

XR great rhombic dodecahedron (c)
One highlighted face
XR great rhombic dodecahedron (d)
One highlighted face
Crossed-Rectangular Medial Rhombic Triacontahedra

XR medial rhombic dodecahedron (a)
One highlighted face
XR medial rhombic dodecahedron (b)
One highlighted face

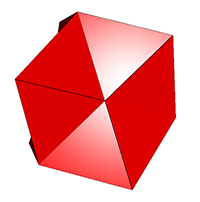
One further example can be obtained from the cube, although in this case the crossed-squares lie in coplanar pairs.  Each square of the cube is replaced by two complimentary crossed-squares.  In the image and link below, half of the crossed-squares have been highlighted for clarity, although the figure is isohedral and isogonal and so could be regarded as a somewhat degenerate noble polyhedron.
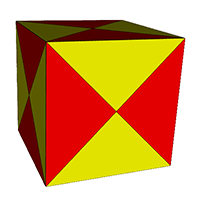XR cube

Further Resources

A Zip file containing all of the polyhedra referenced on this page is HERE.  This contains OFF, Stella (*.stel), VRML (*.wrl) and HEDRON input files (*.txt).  In order to get the VRML files to display correctly, it was necessary to triangule the models such that each crossed rectangle is represented by two separate triangular faces.  Triangulated models in the Zip file are denoted with a '(t)'

Credits

This page was made possible using Robert Webb's excellent Great Stella program (www.software3d.com).  Thanks are due to Roger Kaufman for his VRML2OFF utility, and to Scott Vorthmann for his VRML Revival project.

All VRML files were generated using Great Stella and post-processed with VRML2OFF and HEDRON.

References

1.  H.S.M. Coxeter and B.Grunbaum ,  “Face-Transitive Polyhedra with Rectangular Faces”   C.R. Math. Rep. Aced. Sci. Canada 20, 16-21, 1998 retrieved from https://www.math.ucdavis.edu/~deloera/MISC/LA-BIBLIO/trunk/Grunbaum2.pdf on 01/09/2025.

2.  H.S.M. Coxeter and B.Grunbaum ,  “Face-Transitive Polyhedra with Rectangular Faces and Icosahedral Symmetry”   Discrete Comput Geom 25: 163-172, 2001 retrieved from https://link.springer.com/content/pdf/10.1007/s004540010087.pdf on 01/09/2025.

3.  M. Brückner. "Vielecke und Vielflache: Theorie und Geschichte". Teubner, Leipzig, 1900.  Image retrieved from https://bulatov.org/polyhedra/bruckner1900/index.html on 16/09/2025

Back to index