Arruated
Polyhedra
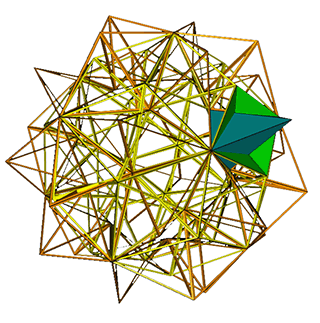
arruated
icosahedron
(4,1)-exo
Inspired by Dr
Richard Klitzing's cuned
twisters[1, Fn 1], I have explored
further polyhedra using an icosahedron as the seed polyhedron.
One method to
generate the desired polyhedron is as follows:
1. Augment faces of
the seed polyhedron with pyramids;
2. Join
the
peaks of egde adjacent pyramids with pairs of triangles; 'wedges'
(effectively filling the valleys with distorted tetrahedra);
3. Relax
the
resulting polyhedron so that all faces are regular
triangles.[Fn 2]
The
effect is to
place one of the above wedges over each edge of the
original polyhedron.
When
George
Olshevsky first described the above process in 2006[2], he
used the term 'spheniated' [Fn 3]. Examples of
Olshevsky's polyhedra can be found on Roger
Kaufman's
site[3]. Mason
Green's cingulated antiprisms[4],
discovered
in
2005
turn
out
to
be
spheniated
prisms
but
Green
used
a
different
method
of
generation.
Green
found
these
by
dividing
an
n-gonal
anti-prism
into
two
equal
sections
each
containing
an
n-gonal
prismatic
cap
and
its
edge
adjacent
triangles,
and
inserting
a
'cingulum'
of
4n
triangles.
They were
rediscovered in 2025 by discord user
'Harsin Sinquin' who used the approach of attaching six triangle
complexes over triangle pairs of the antiprisms, and coming up with the
term "cune". Discussion between Klitzing and Sinquin led
to the cuned twisters.
Both Olshevsky
and
Klitzing's
polyhedra only
consider applying the spheniation/cuning process to a subset of the
edges of the original
polyhedron and some of
the pyramidical faces and original faces of the seed polyhedron
remain. Because of these remaining faces, relaxation of the wedge
faces to equilateral triangles
involves a
'twist' of the remaining faces.
I
decided to explore adding pyramids and wedges to all edges. This means
all the original faces of the seed polyhedron are
augmented and the resulting pyramidical faces have been also been
replaced. This is a generalisation of 'spheniation/cuning' and as
such needed a new term. I
felt a suitable verb would be 'arruo' (to cover with earth or to
bury) hence we get the adjective 'arruated' . The
polyhedra
consist only of the faces of the
wedges. This means
that icosahedral symmetry is preserved and the 'twist' referred to
above is
replaced by the freedom to adjust the height of the pyramids to the
point where an equilibrium is obtained between the edge height of the
pyramids and the distance apart of two edge adjacent pyramids.
In
similar
fashion to the
generation of the Edge
Expanded Bi-Prisms and Bi-Antiprisms, it is possible to
insert more
than one wedge between each peak in step 2 above. I term
the group of wedges between two edge adjacent peaks a 'set'. With more than
one wedge in a set then different configurations can be obtained.
Again it is the height of the pyramids that is adjusted to obtain an
equilibrium. Solutions can also be obtained where the pyramids
have a negative
height, i.e. they are inverted.
The naming
convention is as follows:
- 'n' is
the number of wedges in each set. I also refer to the
collection of polyhedra with 'n' wedges as level 'n'.
- 'exo'
means
the edge angle between the (now virtual) pyramids is less than 180
degrees, 'endo' means the edge angle is reflexive.
- ''w' is
the winding
number, the number of times that the set of triangles winds around an
axis formed by the original edge. The direction of
winding is towards the origin for exo models and outwards from the
origin for endo models.
- The
name is then given as (n,w)-exo/endo.
In
generating the polyhedra below, I used a standard colouring format.
- If sets
consist of one or two wedges they are coloured in
yellow.
- For 3
or 4
wedges per set, the outermost ones are yellow, the inner ones
orange.
- For 5
wedges
per set the colours are as above but the central one is red.
- One set
of wedges is highlighed by having the above colours replaced with
green, cyan and blue respectively. In the VRML files linked
below, these highlighted wedges stay solid through the
'trans/frame/solid' view options.
- This example has 5 wedges per
set and shown before the relaxation step.
- In a number of cases, the internal structure is masked by the
external faces. A 'frame' link has been included which holds tjese
external faces as frames only so that the internal structure can be
viewed more easily.
In a
number of cases the resulting polyhedron is an isohedral deltahedron.
In these cases a link is provided giving the reference in Shephard's
1999 paper on this subject [5].
1. Arruated Icosahedra
Below,
with
notes, is a list of those generated to date with n ≤ 5. I make no claim that
the list is complete, and I would
welcome any further cases. The degenerate cases
may be specific to the seed polyhedron being the
icosahedron.
(1,0)-exo These are
equivalent to replacing
the original polyhedra with
its dual and triangulating the faces. Shephard: I9(2)
(1-0)-endo
The pyramids in
this case do point outwards from the base icosahedron but are so low
that the angle between them is > 180 degrees. Shephard: I9(1)
(2,0)-endo Shephard: I1(2)
(2,0)-exo Shephard: I1(1)
(3,0)-endo This is a
deltahedron.
All
triangular
faces
are
fully
visible.
(3,0)-exo (frame)
(3,1)-endo (frame)
(4,0)-endo (frame)
(4,0)-exo
-
this
is
degenerate,
the
four
wedges
form
faces
of
a
pentagonal
bipyramid
(with
one
open
pair)
and
then
sets
of
wedges
co-incide
in
pairs.
(4,1)-endo
(4,1)-exo
(4.2)-endo (frame)
(4,2)-exo
(5,0)-endo - this
is
degenerate, the five wedges form faces of a pentagonal
bipyramid and the inner vertices are coincident
(5,0)-exo (frame)
(5,1)-endo (frame)
(5,1)-exo (frame)
(5-2)-endo
-
this
may
or
may
not
exist,
I
have
been
unable
to
generate
an
example
(5.2)-exo (frame)
(5,3)-exo (frame)






Don
Romano has modelled the (3,0)-endo
and the (4,1)-exo
arruated
icosahedra. The world's
first physical models of arruated polyhedra.
2. Other
seed
polyhedra
Numerous
polyhedra can act as the seed for this process and I will only scratch
the surface here, although level-1 examples for the Platonic and
Archimedean polyhedra are included in section 3 below.
Each n-goal face of the seed gets augmented with an n-gonal
pyramid, sets of wedges are then inserted as above.
(4,0)-endo
cases (coloured yellow and orange as above) are presented for the tetrahedron, octahedron (degenerate), cube and dodecahedron
(the last two are deltahedra).
As the (1,0) cases
involve the dual of the seed, I also tried starting with a dual.
These are the (4,0)-endo cases for the rhombic dodecahedron (seed) and the rhombic triacontahedron (seed) . The red
faces are
adjacent to the 4 or 5-fold
vertices, the
hidden yellow faces are adjacent to the 3-fold vertices, central wedges
are interpolated between them. Here also is an n=4
case for the rhombic enneacontahedron
(seed), wedges adjacent
to 6
fold vertices are blue, 5 fold are red and 3-fold are yellow, central
wedges are again interpolated.
With more than one type of pyramid present, the endo/exo
categorisation gets more involved and can be mixed in a single
polyhedron. Examples are linked (with no
attempt at categorisation) for the n=3
case for the icosidodecahedron
(seed), the small
rhombicosidodecahedron (seed) and the snub
icosidodecahedron (seed)
In
all
cases
the
colouring
convention
is
use the seed face for the pyramid as the colour
for adjacent wedges and to use an interpolated colour for the centre
wedge. See the links to the seed polyhedra for the case
colours.
Further combinations are possible where there is more than one edge
type to the seed polyhedron. An example was also generated (here) for the small
rhombicosidodecahedron with sets of three wedges between the pentagonal
and square pyramids, and sets of two wedges between the square and
triangular pyramids. I term this type of
arruation a 'level-hybrid'.



Don
Romano has modelled the (4,0)-endo cube.
3.
Partial
Arruation
of the Platonic and Archimedean polyhedra
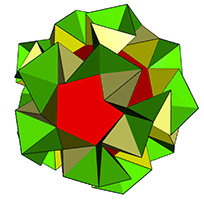
Partially
arruated
(3-s
&
s-s)
snub
icosidodecahedron
Where a
polyhedron has more than one edge type, there is the possibililty of an
intermediate process between Olshevsky's spheniation and
arruation. I term this 'partial arruation'.
In a partially
arruated polyhedron, some but not necessarily all of the edges have
been augmented with wedges. Unlike spheniation, the wedges need
not be distinct, and the face pyramids can form part of multiple
wedges.
The level-1
partial arruations have been explored for all of the Platonic and
Archimedean polyhedra. The endo/exo distinction is not so clear
in some cases as the distortion caused in the relaxation process can at
times be significant. For all cases below, exo/endo notation
refers to the start point where the exo mode has all of the pyramids
everted (outwards) from the seed polyhedron
(for faces with 6 or more edges the pyraimds are elongated), endo mode
has them inverted. The
edges are identified by their adjacent faces, so a 3-5 edge would be
between a triangle and a pentagon. For the snub polyhedra, the
snub triangles are represented with 's'. The colours are taken
from the seed polyhedron (red, blue and yellow) with wedges being an
intermediate colour (green, cyan and magenta). Where the two
adjacent faces are alike, the wedges are grey. Where the text is
struck out, the example was either degenerate or could not be formed.
Level 1 arruation where all edges have been replaced can also be seen
as the dual of the seed polygon which has then been triangulated and
relaxed, partial arruations do not have such a simple
alternative. As a result, for seed polyhedra with one edge type
the results are
fairly trivial. For two or three edge types some interesting
results are obtained but as mentioned above the relaxation stage can
introduce significant distortion. There is also the
possibility of further isomorphs being generated from different start
points where there is a mixture of everted and inverted pyramids.
These have not yet been explored here.
In a number of cases, the anticipated result was not achieved.
This may be due to any of (i) the case does not exist, (ii) the case
exists but the chosen starting point is not one that relaxes to it.
- Where the relaxation stage failed, the text is struck
out. It is my opinion that these cases do not exist.
- Where the endo mode says 'see exo', both starting points
resulted in
the same polyhedron.
- Where the result has coplanar faces it is marked with a (C),
these involve three coplanar triangular faces forming a trapezoid.
- Some cases resulted in degerate solutions with multiply
coincident
faces These are marked with a (D)
One edge type:
Fn 1: Relaxing the polyhedra generated by everting and inverting the
pyramids results in the same polyhedron, which I here have termed
'exo'. It is possible to generate the 'other' example (of the
triangulated dual) through the arruation process but only with
carefully chosen values for the height of the pyramids. The
Shephard reference to these can be obtained by replacing the (1) in the
exo reference to a (2).
Two edge types:
Fn2: There
are multiple vertices coincident at the centre.
Fn3: With
unit length pyramids, the exo mode has coplanar faces
and the endo mode fails to relax. The example linked can be
generated from very low inverted or everted pyramids.


Don
Romano
has
modelled
the
fully arruated endo truncated
octahedron
Three Edge
Types:










Don
Romano has modelled (i) the partially arruated s-s exo snub
cuboctahedron, (ii) the partially arruated 3-s & s-s exo
snub cuboctahedron,(iii) the fully arruated exo snub
cuboctahedron and (iv) the
partially arruated 4-6 exo great
rhombicuboctahedron.
4. Higher
Order Spheniated Polyhedra

(3,1)-endo spheniated snub
icosidodecahedron
Olshevsky's spheniated polyhedra can be regarded as an order 1
spheniation, with one wedge inserted between adjacent pyramids.
In similar fashion to the arruated polyhedra, higher order spheniations
can be obtained by inserting more than one wedge between the
pyramids.
Using the snub icosidodecahedron as an example, spheniations up to
order 3 have been explored. In the examples below, the remaining
pyramidical faces on the snub triangles are coloured pale yellow.
Inserted wedge faces are coloured yellow and orange as in the arruated
polyhedra above.
(1,0)-endo
(2,0)-endo
(2,0)-exo
(3,1)-endo
(3,1)-exo
Attempts to generate (3,0) examples resulted in degenerate polyhedra
with coplanar faces.



Don
Romano has modelled the (3,1)-exo-snub cuboctahedron.
5. Antiprismatically Arruated Polyhedra
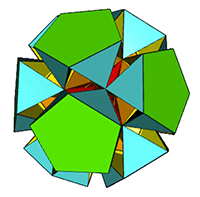
Antiprismatically
arruated
dodecahedron
(5,0)
exo
A second family
of arruated polyhedra exists. Rather than
augmenting the faces of the seed polyhedron with pyramids, augment
instead with antiprisms. Then connect the outer vertices of the
edge connected antiprisms with wedges and relax them. Olshevsky [2]
uses the term 'ambiation' to mean this process applied to a
single face. The process of antiprismatic arruation is thus a
generalisation of Olshevsky's ambiated polyhedra in the same way that
the (pyramidically) arruated polyhedra are a generalisation of his
spheniated polyhedra.
Applying one set
of wedges does not result in any polyhedra of
particular interest. The remining triangular faces of the
antiprisms and the wedge faces become complanar and form
hexagons. As an an example, the (1,0)
anitiprismatically arruated dodecahedron then becomes a
partially
triangulated truncated icosahedron.
The
level-1
examples
are
somewhat
related
to
the
monorhombal
edge
rhombified
polyhedra with the rhombi being split into two
equliateral triangles.
With two or more
sets of wedges the results become more interesting, I
have explored these for levels 2 and 3 for the platonic polyhedra, with
some additional focus on the dodecahedron where I have explored up to
level 5.
The naming
convention is consistent with that above. The colour
convention is that the upper faces of the antiprisms are green, the
remaining lateral antiprismatic faces are cyan, the wedge faces are
yellow, orange and red as in the (pyramidically) arruated
polyhedra. Where the text is shown in red and struck out, the
example is either degenerate or does not exist. Where the text is
black and unlinked, I have not been able to generate the example, but
cannot rule out that it exists.
Seed
|
Level 2
|
Level 3
|
Tetrahedron
|
(2,0)-exo
(2,0)-endo
|
(3,0)-exo
(3,0)-endo
(3,1)-exo (frame)
(3,1)-endo |
Octahedron
|
(2,0)-exo
(2,0)-endo (frame)
|
(3,0)-exo
(3,0)-endo (frame)
(3,1)-exo (frame)
(3,1)-endo (frame)
|
Cube
|
(2,0)-exo
(2,0)-endo (frame)
|
(3,0)-exo
(3,0)-endo
(3,1)-exo
(3,1)-endo
|
Icosahedron
|
(2,0)-exo
(2,0)-endo (frame)
|
(3,0)-exo (frame)
(3,0)-endo (frame)
(3,1)-exo (frame)
(3,1)-endo (frame)
|
Dodecahedron
|
(2,0)-exo
(2,0)-endo |
(3,0)-exo
(3,0)-endo
(3,1)-exo
(3,1)-endo |
Level 4
dodecahedra: (4,0)-exo
, (4,0)-endo , (4,1)-exo , (4,1)-endo , (4,2)-exo ,
(4,2)-endo
Level 5
dodecahedra: (5,0)-exo
(frame) , (5,0)-endo , (5,1)-exo (frame) , (5,1)-endo (frame) , (5,2)-exo ,
(5,2)-endo , (5,2)-exo , (5,2)-endo
I have also
explored some antiprismatic arruations of the icosidodecahedron. In
these cases the term nendo refers to the
n-gonal antiprism
being inverted or everted.
I have to date
been unable to generate any level 3 examples.








Don
Romano has modelled (i) the antiprismatically
arruated
(3,0)
exo
tetrahedron, (ii) the antiprismatically arruated (2,0) exo
cube,
and (iii) the antiprismatically arruated (2,0)
endo dodecahedron.
6.
Hybrid
arruation
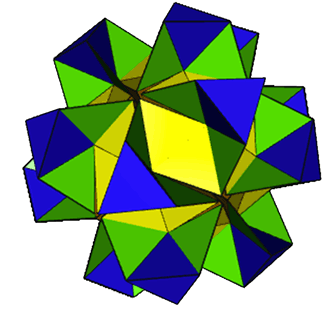
It is possible
to mix the two forms of arruation in a single process and successfully
relax the resulting polyhedron to only contain regular faces.
Each face type of the
seed polyhedron can be left as is, augmented with pyramids or augmented
with antiprisms, these can be outward or inward facing.
Each edge type can then be left as is or replaced with a number of
wedges.
For the snub icosidodecahedron level-1, with one edge replaced only two
of the three face types are augmented so we have 3 edge types and 42
orientations, with two or
three edges replaced all faces are augmented so there are (3+1)x43
orientations. This makes 304 starting orientations in
total. The same count can be arrived at for level-2. For
level-3 there are both the (3,0) and (3,1) cases so there are 608
orientations. 1216 starting orientations in total
Now considering also the prospect of level-hybrids (see section 3
above) we need a minimum of two edge types replaced so all faces must
be augmented. The first edge type can be
any one of 4 levels (incuding (3,0) and (3,1) as separate cases) the
second any of the remaining 3. So we have 3 choices of edge pairs
each
with 12x43 starting orientations (2304 in total). With
three
edges repaced we have 43-4 level options (we must omit the 4
where the levels are all equal as they were added above) with 43
orientations
(3840). This makes a total of 1216+2304+3840 = 7360 possible
starting orientations. Not all will result in valid distinct
polyhedra as some will not relax, some will be coplanar or degenerate
and some will form duplicates.
Just one
example fom the above 7360 have been generated - linked from the image
above. It has the
icosahedral triangular
faces augmented with antiprisms, and the pentagonal and snub triangular
faces augmented with pyramids. All edges have been replaced with
one set of wedges. All augmentations are outwards
so is an
'exo' case.
7. Credits
and
Resources

My thanks to Dr
Richard Klitzing for providing the inspiration for this page and to Don
Romano for his boundless enthusiasm and modelling skills.
The
augmentation
of
the
seed
polyhedra,
creation
of
the
nets
and
initial
relaxation
was
performed
using
Great
Stella.
Stella VRML files were
then
converted into HEDRON input files using
Roger
Kaufman's VRML2OFF
utility.
Then
final
relaxation
and
VRML
generation
using
HEDRON.
Some
of
the
cases
were
generated
using
an
excel
spreadsheet
to
spherically
invert
the
vertex
locations.
The
spreadsheet
is
included
in
the
zip
file.
A zip file containing TXT and OFF files for all polyhedra on this page
is here.
Footnotes
[Fn 1] In Latin,
the word cuneus (plural cunei), means a wedge or a
wedge-shaped object, area, or formation. This term is the source for
words like "cuneiform" (wedge-shaped writing) and "cuneus" (a
wedge-shaped part of the brain) and is a root of many English words
describing wedge-shaped forms! (Google)
[Fn 2] Relaxing a
polyhedron refers to the process of iteratively adjusting
the locations of a polyhedron's vertices such that they meet a set of
predefined criteria (e.g. all edge lengths are equal and they form
regular faces).
[Fn 3] The
prefix "spheno-" originates from the Greek word for "wedge" and refers
to something wedge-shaped or of or relating to the sphenoid bone, a
wedge-shaped bone at the base of the skull. Examples of its use include
sphenogram, meaning a wedge-shaped character, and sphenopalatine, which
refers to the sphenoid bone and the palate. (Google)
[Fn
4] Olshevsky [2]
also describes a process he terms 'ambiation'. To quote
Olshevsky:
"Ambiation
is
a
generalization
of
spheniation
to
a
patch
of
more
than
two
faces.
Specifically, the
patch is a regular n-gon surrounded on all sides by n equits
[equilateral triangles]"[2]. This process is
different from the process I am describing here.
[Fn 5] For more on Stress Maps see here
References
1
Klitzing, R. (2025) Cuned Twisters. https://bendwavy.org/klitzing/explain/twisters.htm#cune
2.
Olshevsky
G.
(c2006) Breaking Cundy's Deltahedron record
(unpublished) linked from [3] below.
3. Kaufman R. (2008) The Cundy Deltahedra. https://www.interocitors.com/polyhedra/Deltahedra/Cundy/index.html
4. Green, M. &
McNeill J. (2005) Cingulated
Anti-prisms https://www.orchidpalms.com/polyhedra/chiral-prisms/prisms9.html
5.
Shephard G.C. (1999) Isohedral Deltahedra, Periodica Mathematica
Hungarica Vol. 39 (1-3), 83-106
Back: to index






































