Pentakis Icosidodecahedra

My exploration as to which Archimedean polyhedra can be used as a 'seed' to generate families with prismatic symmetry which can take various n-gonal polyhedra as their bases included consideration of the icosidodecahedron. In this instance both the pentagonal faces and the triangular faces can be regarded as the base.

Pentagonal base

In the same way that the icosidodecahedron can be regarded as the fusion of two pentagal rotundae, the n-gonal pentakis icosidodecahedron pentagonal base can be regarded as the fusion of two pentakis rotundae, although for n <> 5 the name 'icosidodecahedron' is something of a misnomer and perhaps the term 'n-gonal birotunda' would be more appropriate.

I have again concentrated my examples to date around n=7.

Variations exist with (i) star polygons as bases, (ii) inverted pentagonal prisms, (iii) elongated and gyro-elogated forms, (iv) 'ortho' and 'gyro' modes. These have with one exception not been explicitly generated as they are easy to create from the pentakis rotundae.

n=7, everted pyramids

Triangular base

The situation here is more complex as these cannot be regarded as combinations of rotundae. The name of n-gonal pentakis icosidodecahedron triangular base will have to suffice until something more appropriate is suggested.

Two examples of this family have been generated for n=7, with the pentagonal prisms pointing outward and inward. Both are highly distorted from the originating icosidodeahedron. Some star polygon variants have also been generated. I attempted to make both inverted and everted models for polygons from {7/2} to {7/6}. If the eample is not shown below, then I was not able to generate that variant.

n=7, everted pyramids	n=7, inverted pyramids
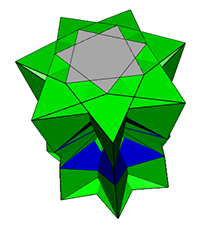n=7/2, everted pyramids. May have degenerate vertices.	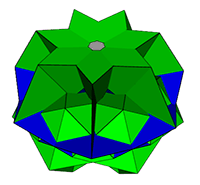n=7/3, everted pyramids.
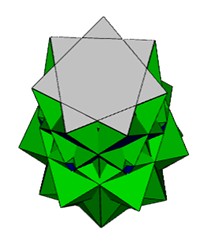n=7/5, everted pyramids.

These polyhedra were generated using Great Stella, Antiprism and HEDRON.