Flying Further into the K5 Galaxy
An extension to Chapter XVI of 'Adventures Among The Toroids' by B.M.Stewart 

4. A Solution to Stewart Exercise 153


At the conclusion of Ex 153 on p193 Stewart poses the unsolved problem of passing a Z4(Z4(P4)Z4)Z4 rod through P'' (link) (the hole of the Zulu Chair - or 'footstool').

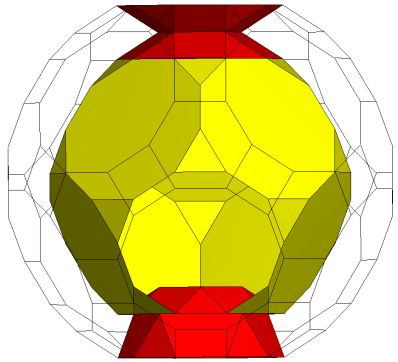
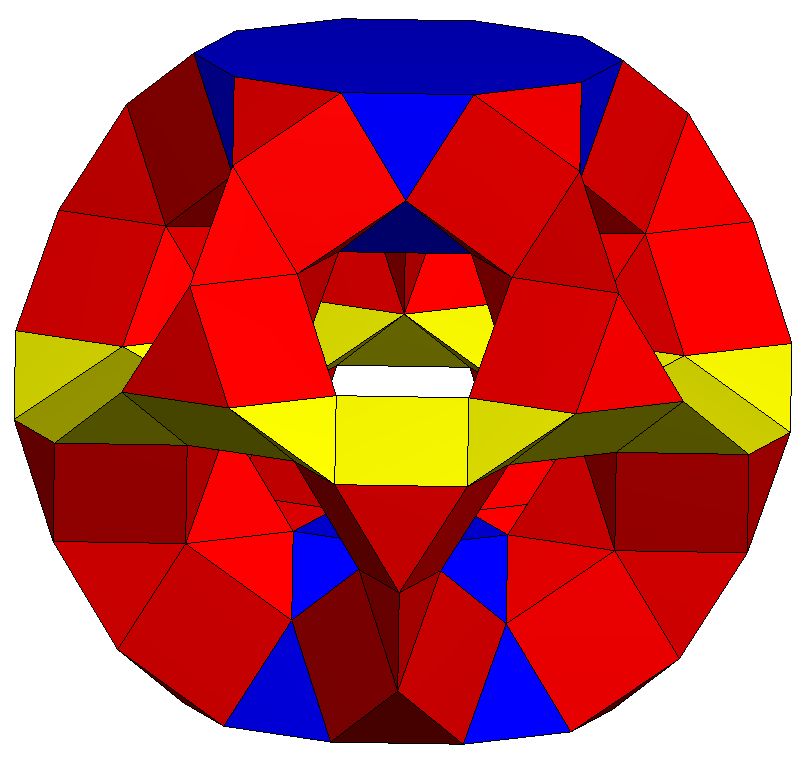
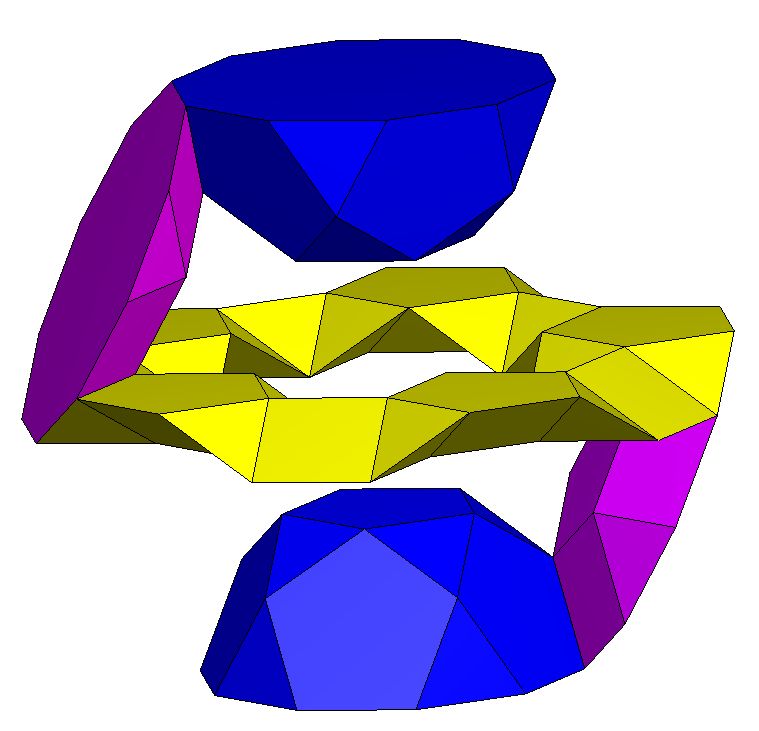
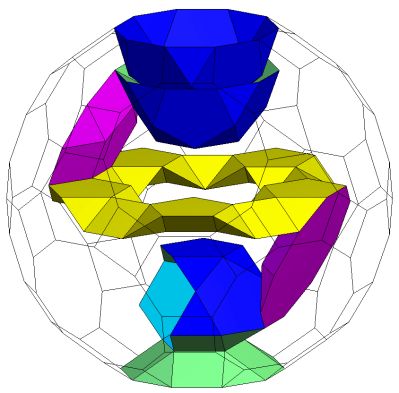
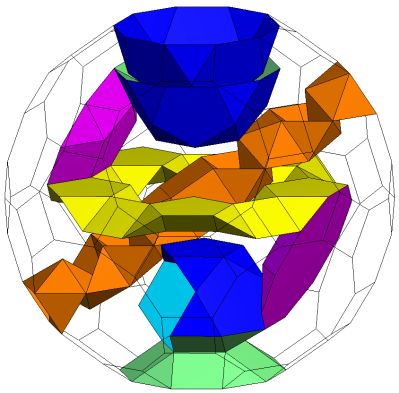
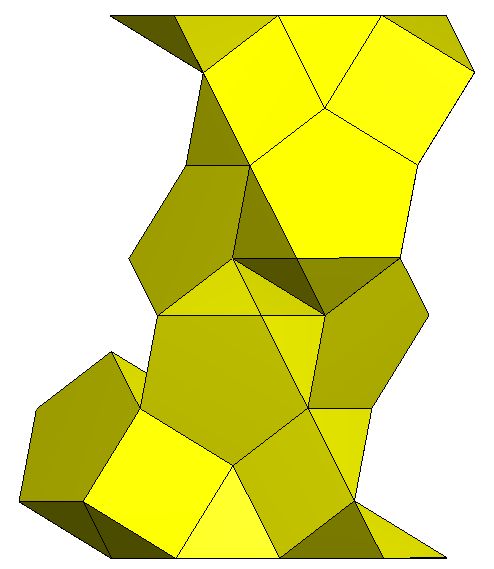
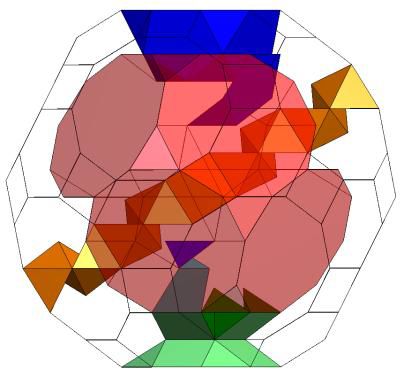
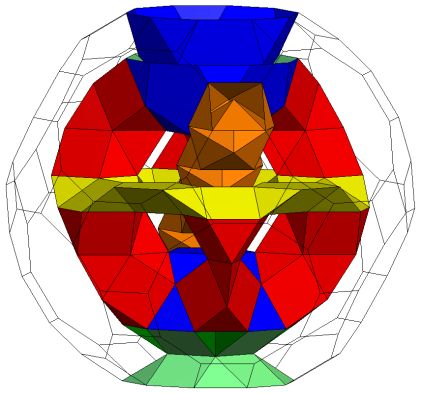
The solution to this was inspired by the discovery of the rather simple toroid K5 / T5Q5S5Q5 which is implied in Stewart as the basis of the Zulu chair discussion but is not explicitly described.


K5 / T5Q5S5Q5.   Genus p=1

The solution involves:
(i) moving the T5 to be nearly central to the containing K5
(ii) replacing the T5 with a 'stripped down' version of the tunnel from T5 / 12Q5S5(D5) leaving a relatively open P'' through which the rod can be passed and
(iii) resolving minor interference issues.

Part (i) is achieved by replacing the S5 with the combination R5Q5A and putting it at the other side of the T5 to form K5 / R5Q5AT5Q5Q5. This appears in Stewart on page 148. Note that despite initial appearances the T5 is not quite central to the K5.


K5 / R5Q5AT5Q5Q5.   Genus p=1
One decagon in T5 has been removed to show the internal structure.

Turning now to part (ii), on pages 176-179 Stewart describes the toroid P* - or T5 / 12Q5S5(D5)


T5 / 12Q5S5(D5)  with P" shown in yellow, C in red and R5 in blue.  
Genus p=11.

Implied in this section is a dissection of T5 into 2R5 • 10Q5 • 10S5 • 10C • P" • (D5) where P" is ring described on page 179 and shown in yellow above. C is my term for one of the 'containers' which Stewart describes but does not name


C


The two copies of R5 and P" can be joined in a number of ways (more on this later) but the simplest involves leaving just two opposing copies of Q5 to form R5Q5P"Q5R5


R5Q5P"Q5R5


This combination can then replace the T5 in K5 / R5Q5AT5Q5Q5 and a Z4(Z4(P4)Z4)Z4 threaded through the hole in P''.

Part (iii). As the T5 was not central to the K5, the rod clears one R5 but not the other. To resolve this, excavate J91 from the R5Q5 combination opposite the link to C. The result is shown below (a) without the rod, and then (b) with the rod. The resulting toroid is then K5 / R5Q5AR5Q5P''Q5R5Q5J91-EQ5 , Z4(Z4(P4)Z4)Z4.


K5 / R5Q5AR5Q5P''Q5R5Q5J91-EQ5
Genus  p=2

A solution to the problem posed at the end of Ex 153:
K5 / R5Q5AR5Q5P''Q5R5Q5J91-EQ5 , Z4(Z4(P4)Z4)Z4.
Genus p=3.


The clearance between the rod and the ring is shown by a cross-section through the centre of K5


Cross section through the centre of
K5 / R5Q5AR5Q5P''Q5R5Q5J91-EQ5 , Z4(Z4(P4)Z4)Z4

Given that there were choices in how to join the two copies of R5 and P", it is interesting to see how much of the original T5 can be re-instated without the tunnels interfering. We can keep 2R5, 8Q5, 4S5, 6C and P" removing just 2Q5•6S5•4C•(D5)


2Q5•6S5•4C•(D5) the minimal hole through T5 which still allows threading by Z4(Z4(P4)Z4)Z4

With coplanarity issues resolved by excavating three copies of Y3 the resulting toroid becomes K5 / R5Q5AR58Q54S56C(P'')R5Q5J91-EY3-3Q5 , Z4(Z4(P4)Z4)Z4


K5 / R5Q5AR58Q54S56C(P'')R5Q5J91-EY3-3Q5 , Z4(Z4(P4)Z4)Z4
Faces formed from T5 are translucent.


Despite appearances the rod (orange) and the excavated J91 (pale blue section of the tunnel) do not intersect as can be seen in the above image.

A further toroid of interest arises by keeping 2R5, 6C and P". These then form a cage through which the Z4(Z4(P4)Z4)Z4 rod can pass (again three copies of Y3 have to be excavated to avoid coplanarity.) With genus p=7, this appears to be the highest genus example for this family of toroids.

K5 / R5Q5A2R56C(P'')Q5J91-EY3-3Q5 , Z4(Z4(P4)Z4)Z4; Genus p=7.