Flying
Further
into
the K5 Galaxy
An
extension
to
Chapter
XVI
of
'Adventures
Among
The
Toroids'
by
B.M.Stewart
In his work ‘Adventures Among the Toroids:
A study of Orientable Polyhedra with Regular Faces’, [1]
Professor B.M. Stewart (1980) introduced a family of toroidal polyhedra
which would become synonymous with his name.
The Stewart toroids as
they would become known are polyhedra (‘P’) meeting the following four
conditions, which Stewart sets out in Chapters II and VIII:
(R): each face of P is a regular polygon
(A): faces of P which share an edge are not coplanar
(Q): every edge of the convex closure of P is an edge of P. (The ‘Q’
represents the term ‘quasi-convex’)
(T): a subset of the faces of P forms at least one ‘tunnel’ through P
amending its genus. This last condition is more formally defined by
Stewart on page 75.
Since the second edition of Stewart’s work in 1980, the only extensions
have been by W. Alex Doskey (2002) [2]
and by Robert Webb (2003) [3].
Doskey and
Webb introduced several toroids which, while they met the four
conditions (R)(A)(Q)(T) above, had faces in the convex closure that
were not themselves regular. Stewart had considered this possibility
but deliberately restricted himself to polyhedra where the convex
closure only has regular faces, a condition that Stewart termed (Q").
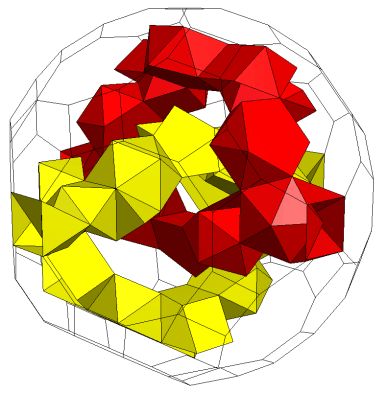
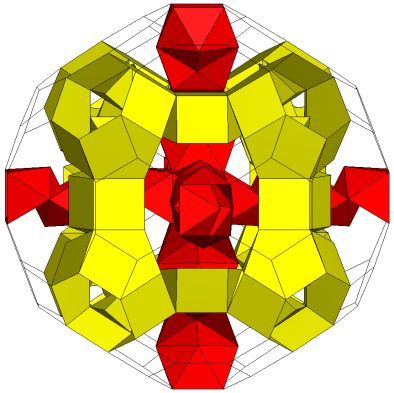
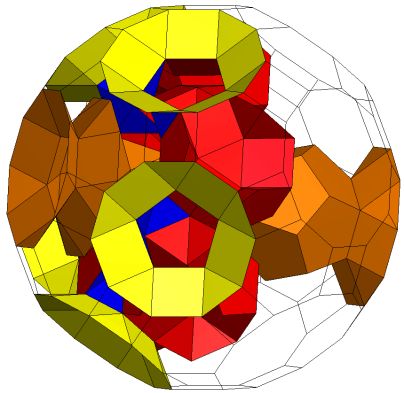
On these pages I present a number of new Stewart toroids that meet
Stewart’s stricter (R)(A)(Q")(T) conditions. All have the convex
closure of a truncated icosidodecahedron, in Stewart's terminology K5.
In
sections
1
to
4,
I
present
toroids
with
interesting
properties including:
(i) up to six
independent tunnels,
(ii) tunnels passing through others up to six
times,
(iii) interlinked tunnels, and
(iv) a genus p=53 Stewart
Toroid.
In section 5, I provide a
solution to the problem posed at the end of Ex 153, which Stewart was
not able to solve, i.e. that of passing a Z4(Z4(P4)Z4)Z4
rod through the hole of the "Zulu Chair". I then explore variations on
this solution.
Glossary
Names are from Stewart except
those denoted with # which are my own additions.
A5 - Stewart A5 - (Stewart page 154)
A5''
- Stewart A5'' - (Stewart page
156)
C - the 'container'
polyhedron
in
T5 / Q5S5(D5)
described
by
Stewart
(page
178)
but
not
named
#.
D5 - dodecahedron.
E5 -
rhombicosidodecahedron.
gQ5 - gyrated pentagonal
cupola.
gZ4 - Gyrated Stewart Z4
– (Stewart page 132). Specifically
when
excavated
from
E5 such that the symmetry axis of the Z4
is parallel to the square-decagon edges of E5.
G3 - Stewart
G3
– (Stewart page 129).
I5 - icosahedron.
J63 - tridiminished
icosahedron.
J91 - bilunabirotunda.
J92 - hebesphenorotunda.
K5 - truncated
icosidodecahedron.
m - Stewart
m –
(Stewart page 156).
Stewart also uses m for 'meta' orientations, but this usage does not
appear in this paper.
m* - Stewart
m* -
(Stewart page 156)
P'' - a
ring polyhedron forming the
central part of Stewart's "Zulu footstool" – (Stewart page 179).
P4 - cube
Q5 - pentagonal cupola.
R5 - pentagonal rotunda.
S* - a rod made up of Q5S5(S5(gQ52)D5)S5Q5
or any variation on such - see section 1 #.
Sn - n-gonal antiprism.
T5 - truncated
dodecahedron.
W - Stewart
W –
(Stewart page 169).
W" - Stewart
W" –
(Stewart page 168).
W+ - the complex WY3-6
- see section 2 #.
X - Stewart
X –
(Stewart page 134).
Yn - n-gonal pyramid.
Z4 - Stewart Z4
– (Stewart page 132).
A
note on nomenclature
These pages follow the nomenclature of Stewart as far as is possible.
However, as Stewart does not contain a nomenclature section, some
aspects of the nomenclature must be collected from the text. The
conventions used in this paper are as follows with X and Y below
standing for any polyhedron or combination of polyhedra:
nX - n copies of polyhedron X forming
separate entrances in the enclosing polyhedron (Stewart page 43).
Multiple polyhedra can follow the n without brackets (Stewart page 43)
Xn - X repeated n times in
a single tunnel. Stewart appears inconsistent in his use of this, e.g. Q32
/ S3S3 (Stewart page 31) and only seems to use it
in the case of Qn2
XnA - X augmented onto the
previous polyhedron n times (1 is omitted) (Stewart page 74)
XA is also used for a
retracted polyhedron (Stewart page 114)
X-nE or X-n - X
excavated from the previous polyhedron n times (1 is sometimes omitted)
(Stewart page 74). The E is sometimes omitted (Stewart page 132)
(X) - X is central to the toroid or
is the inner polyhedron connecting multiple tunnels (Stewart page 16).
X,Y - Two independent tunnels
(Stewart page 116)
n(X) - Where the entire tunnel is
bracketed this means n independent tunnels (Stewart page 188)
pX•qY - The decomposition of a
polyhedron into p copies of X and q copies of Y. This is used in place
of the character ⊕ (Unicode U+2295) used by Stewart as the latter is
not always available.
Extensions
to
Stewart's
nomenclature
[XY]n - The combination of
polyhedra XY in the square brackets is repeated in sequence n times;
XnC or [XY]nC -
X or the combination of polyhedra XY in the square brackets is repeated
in sequence n times and creates a closed ring.
Further Resources
3D models of all the
figures in this paper are available here.
This file contains VRML
(*.wrl), *.OFF, Stella (*.stel) and HEDRON input (*.txt) files.
Credits
This paper was made possible using Robert Webb's excellent Great Stella
program (www.software3d.com)
and by multiple references to Alex
Doskey's Stewart Toroids website (polyhedra.doskey.com/Stewart00.html),
where
he
has
provided
a
most
valuable resource by modelling most of the
toroids in Stewart's book. My thanks also to Dr Richard Klitzing
(bendwavy.org/klitzing/home.htm)
for
inspiration
by
pointing
out
to me
that I had somewhat neglected K5 based toroids this website,
to Roger Kaufman for his
VRML2OFF utility,
and to Scott Vorthmann for his VRML Revival project
which gave me the
motivation to put these pages online.
All VRML files were generated using Great Stella and post-processed
with VRML2OFF
and HEDRON.
References
1. Stewart, B. M.(1980)
Adventures among the toroids: a study of quasiconvex, aplanar,
tunnelled, orientable polyhedra of positive genus having regular faces
with disjoint interiors. Okemos, Mich:Stewart, Print. Page references
are to the Second Edition.
2. Doskey, W.A. (2002) New
Stewart toroids: Exploration of models with irregular-faced convex
hulls, Symmetry: Culture and Science, 13(1-2), 33-46. Also at polyhedra.doskey.com/PrismExpansions.html
3. Webb, R. (2003) A Genus-41 Stewart
Toroid, www.software3d.com/WebbToroid.php
Back: To index