1.1 Six Independent Tunnels
1.2 K5 with ringed tunnels and with
one tunnel passing through another
1.3 Rods including E5
1.4 Very long tunnels and loops
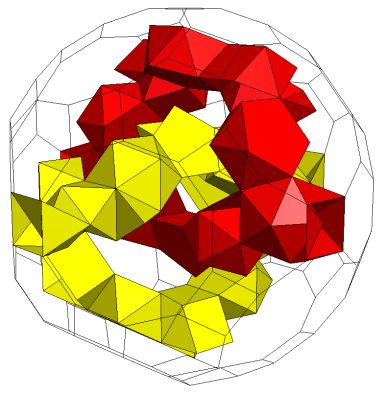
1.5 Two interlinked tunnels
 1.1 Six Independent Tunnels |
 1.2 K5 with ringed tunnels and with one tunnel passing through another |
 1.3 Rods including E5 |
 1.4 Very long tunnels and loops |
 1.5 Two interlinked tunnels |
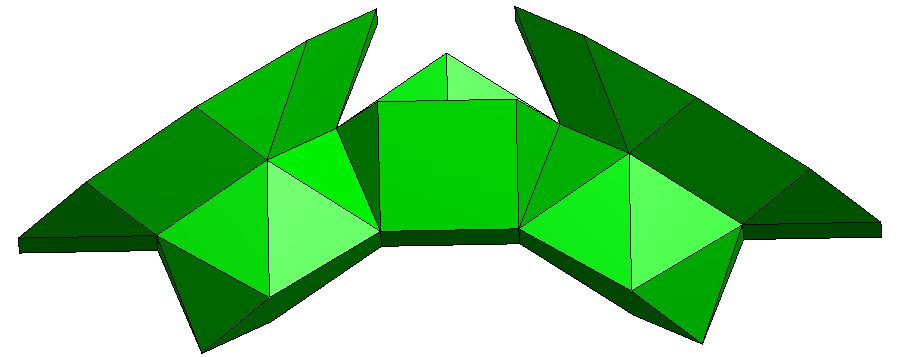 Q5S5(m*)S5Q5 |
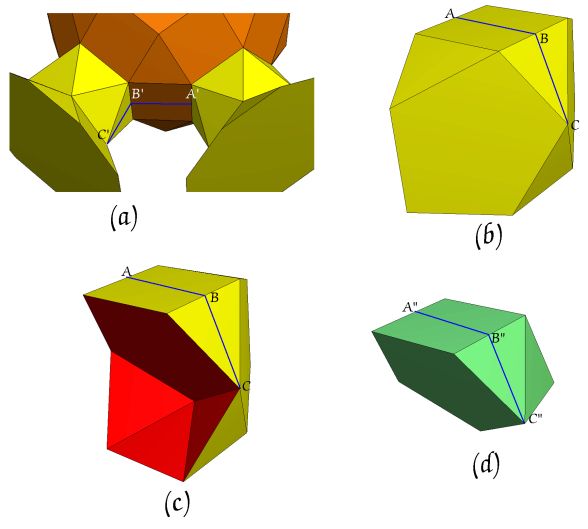 Equivalent dihedral angles (a) A'B'C' in K5 / nQ5S5(E5), (b) ABC in J91, (c) ABC in J91J63-E ,(d) A"B"C" in m* |
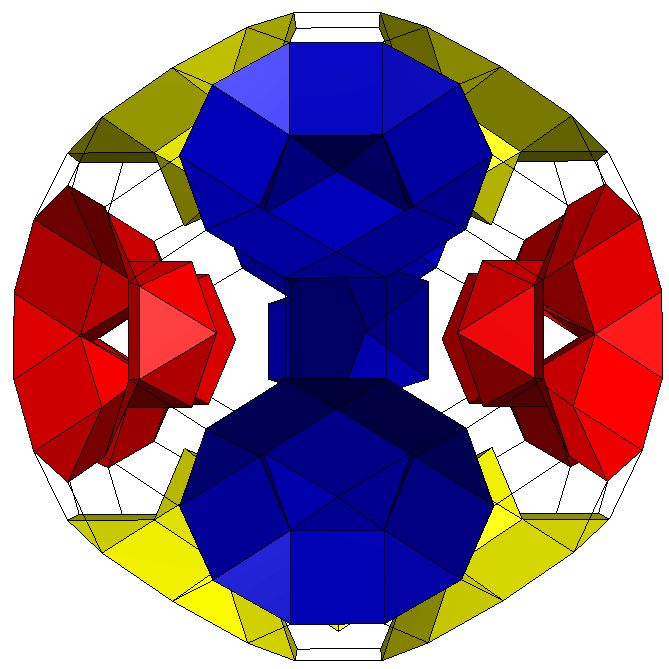
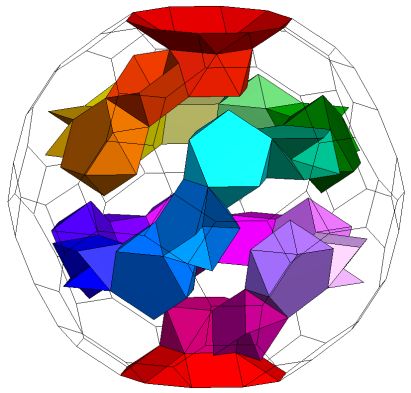
 Toroid with six independent tunnels K5 / 6(Q5S5(m*)S5Q5). Genus p=6 |
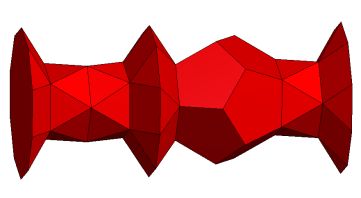 The 'sceptre' or S*, in this instance: Q5S5(S5(gQ52)D5)S5Q5. |
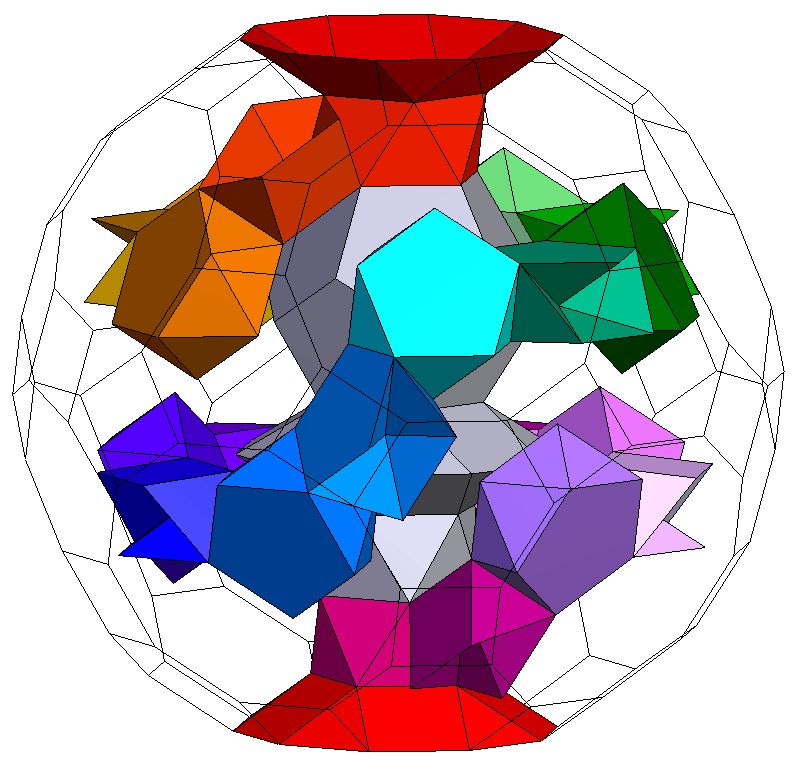
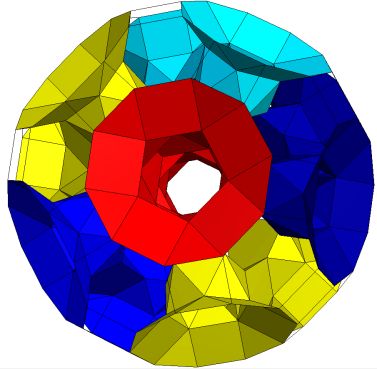 Toroid with six independent tunnels K5/5(Q5S5(m*)S5Q5), S*; Genus p=6. |
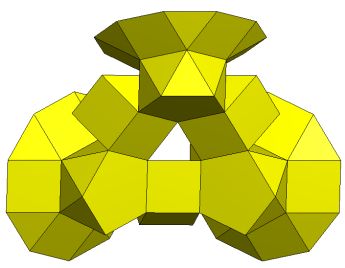 [Q5S5m*]3C |
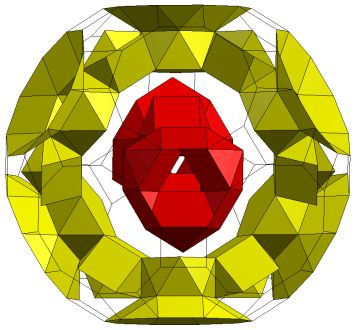
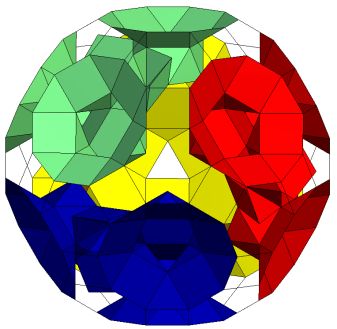 K5/4[Q5S5m*]3C Four independent tunnels. Gensus p=12. |
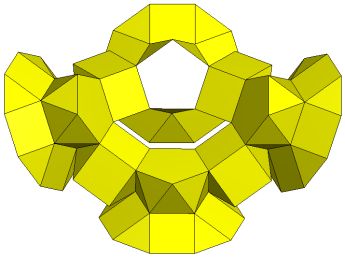 [Q5S5m*]4C Four independent tunnels. Gensus p=12. |
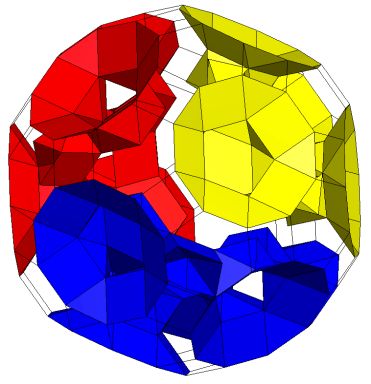 K5/3[Q5S5m*]4C Three independent tunnels. Gensus p=12. |
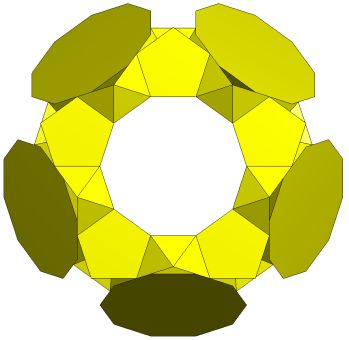 Ring formed by [Q5S5m*]5C |
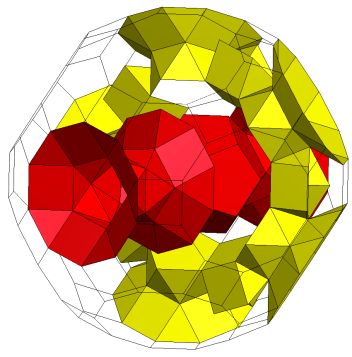 Threaded tunnels K5/[Q5S5m*]5C , S*; Genus p=6. |
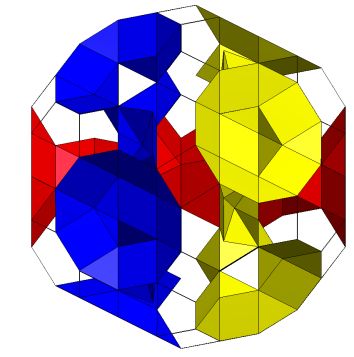 2-fold threaded tunnels K5/2[Q5S5m*]5C , S*; Genus p=11. |
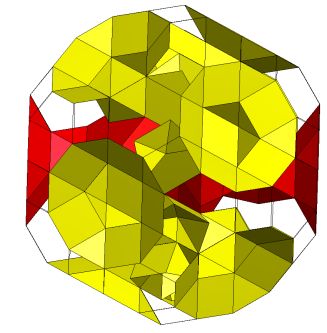 Threaded tunnels K5/[Q5S5m*]10C , S*; Genus p=11. |
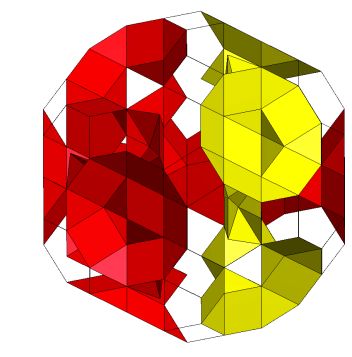 Threaded tunnels K5/[Q5S5m*]5C , [Q5S5m*]5C(S*5m*); Genus p=11. |
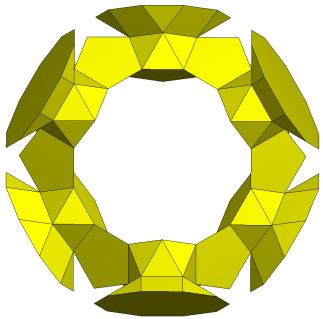 Ring formed by K5/[Q5S5m*]6C |
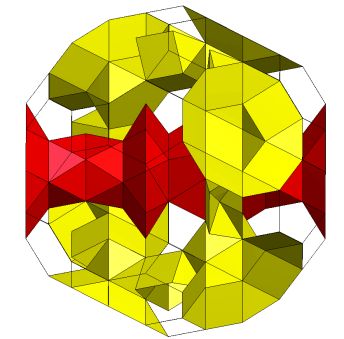 |
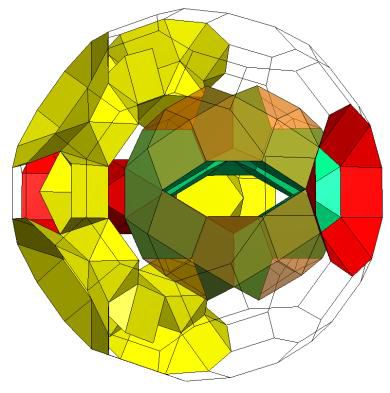
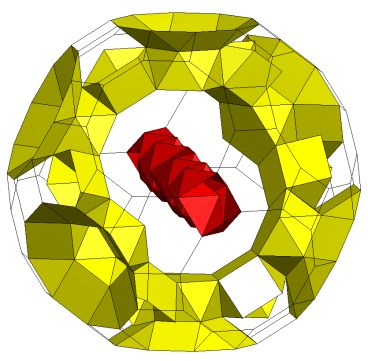 Threaded tunnels K5/[Q5S5m*]6C , Z4(Z4(P4)Z4)Z4; Genus p=7. |
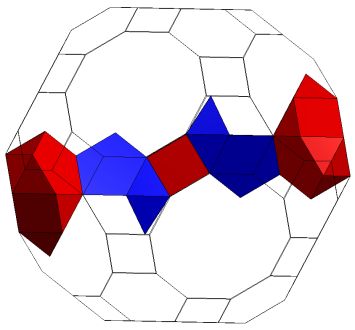 K5/J92(X(P4)X)J92; Units coloured separately for clarity. Genus p=1. |
 |
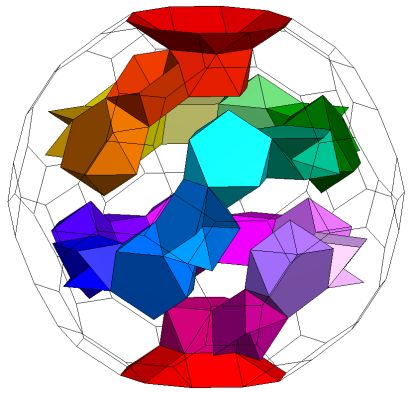
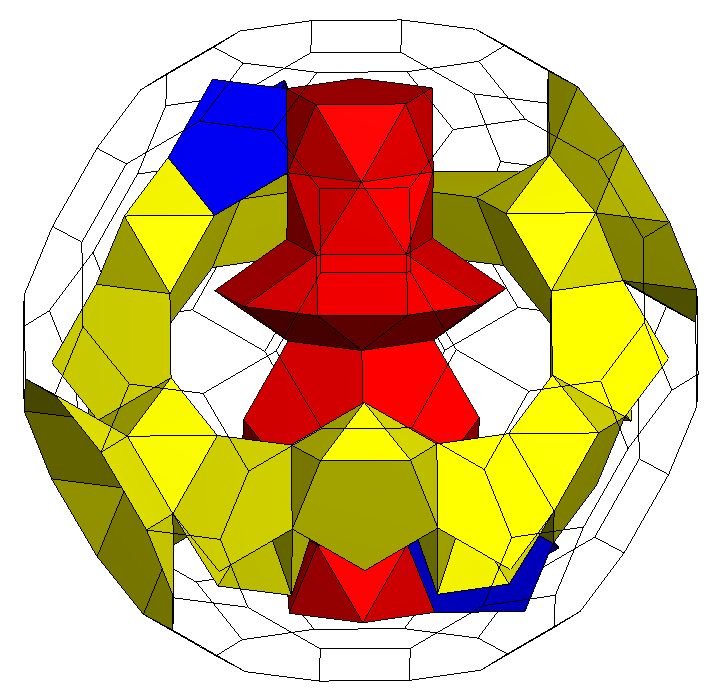 A self-threading tunnel. K5/Q5[S5m*]6CQ5S52Q52D5S5 ;Genus p=3. The 'ring' is shown in yellow. The connecting M* in blue and the S* section in red |
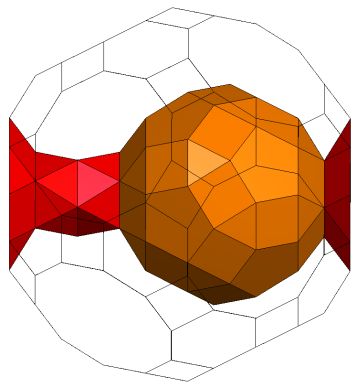 K5 / Q5E5S5S5Q5. Genus p=1 |
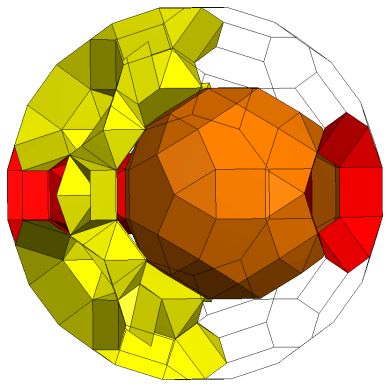 K5 / [Q5S5m*]5C, Q5E5S5S5Q5. Genus p=6. |
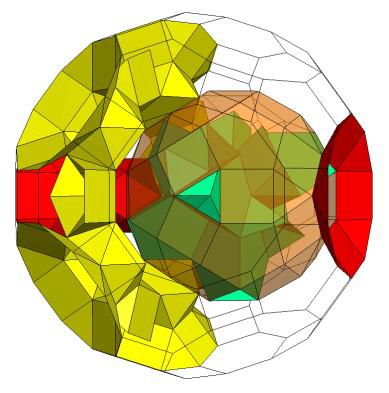 Threaded toroid with rod of genus p=5. K5 / [Q5S5m*]5C , Q5(E5 / 6X (P4))S5S5Q5. E5 translucent to show internal structure; Genus p=11. |
 Threaded toroid with rod of genus p=5. K5 / [Q5S5m*]5C , Q5(E5 / 6J91 (P4))S5S5Q5. E5 translucent to show internal structure; Genus p=11. |
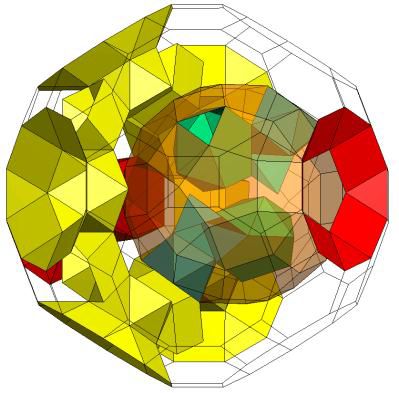 Threaded toroid where rod has two independent tunnels. K5 / [Q5S5m*]5C , Q5(E5 / 2(Z4I5Y5-E))S5S5Q5. E5 translucent to show internal structure; Genus p=8. |
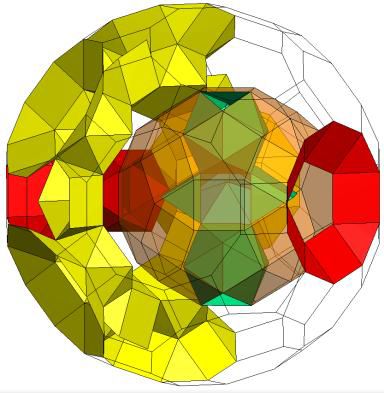 Threaded toroid with two storied rod. K5 / [Q5S5m*]5C,Q5(E5 / I5(J91 / Z4)I5)S5S5Q5. E5 translucent to show internal structure; Genus p=8. |
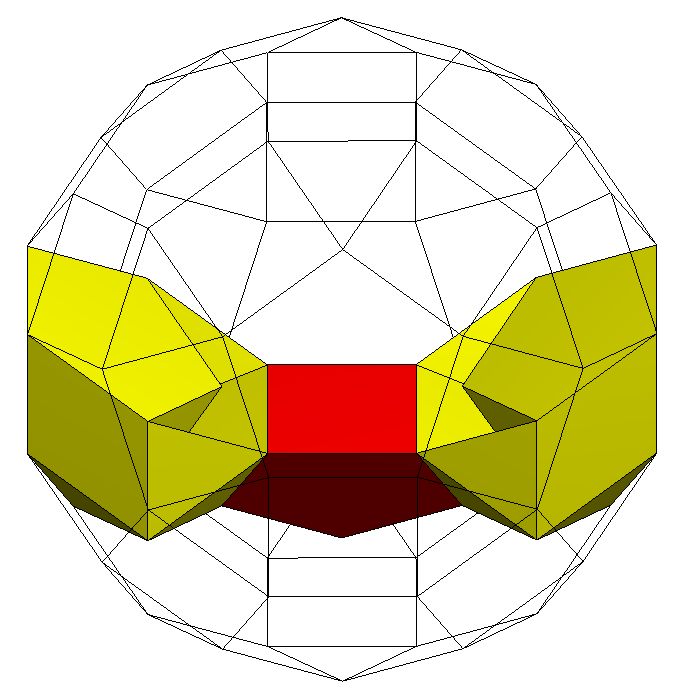
 K5 / Q5[S5m*]11S5Q5 with a tunnel over 22.9 edge lengths long; Genus p=1. |
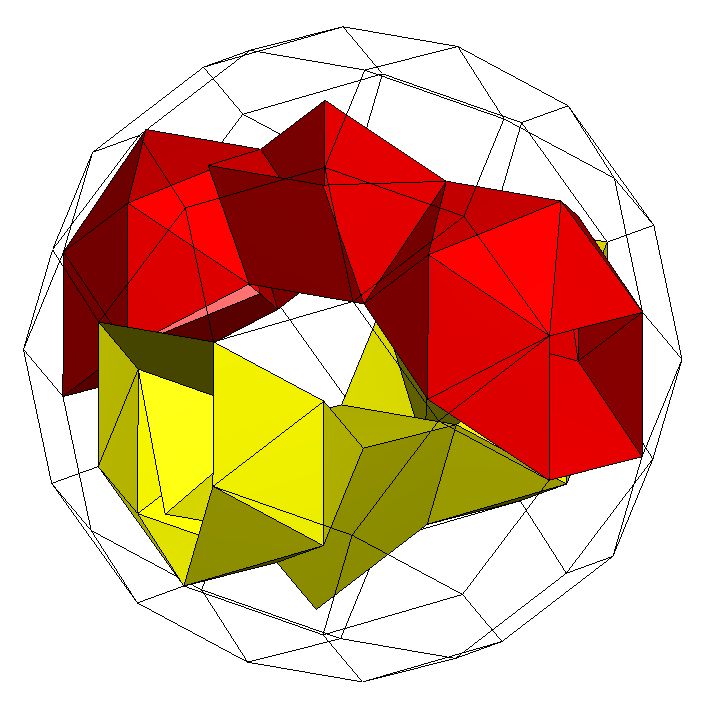
 K5 / Q5[[S5m*]11S5D5gQ52S5]CQ5. The previous toroid with the insertion of the remaining parts of S* creating a loop over 26 edge lengths long; Genus p=2. |
 L4 - shown here inside E5 |
 E5 / 2L4. Not a Stewart Toroid. |
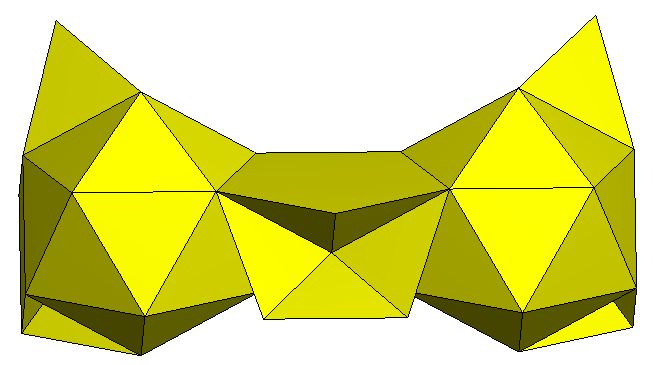 L4* - coplanarity issues resolved. |
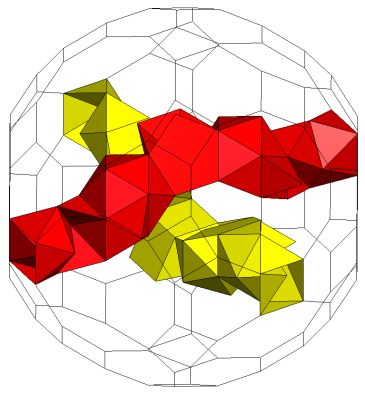 K5 / 2gZ4L4*gZ4;Genus p=2. |
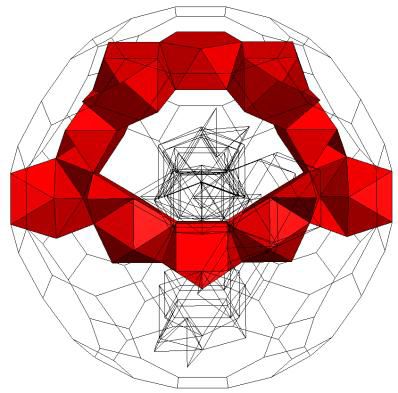 First tunnel K5 / gZ4L4*gZ4[2S5Y3-Em*m*(S5)]C |
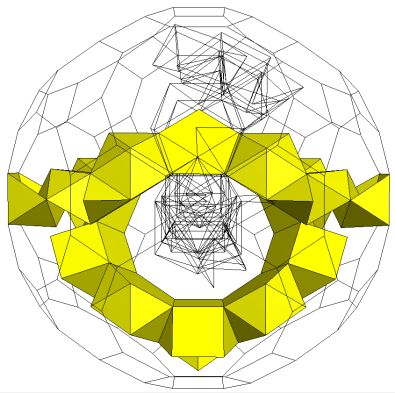 Second tunnel: K5 / gZ4L4*gZ4[2S5Y3-Em*S5(m*)]C |
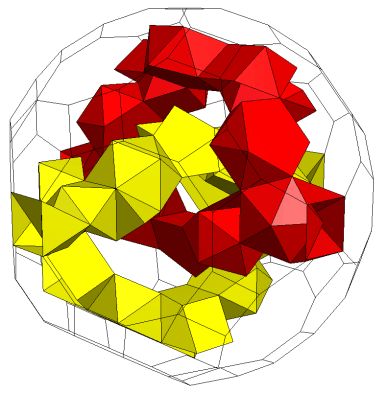 Two interlinked tunnels: K5 / gZ4L4*gZ4[2S5Y3-Em*m*(S5)]C, gZ4L4*gZ4[2S5Y3-Em*S5(m*)]C; Genus p=4 |