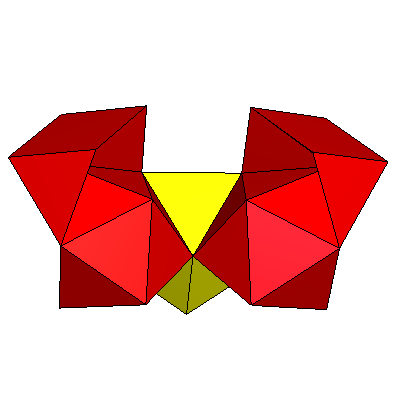
gZ4Y5gZ4
 gZ4Y5gZ4 |
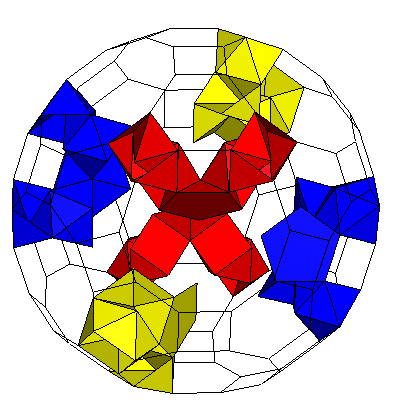 K5 / 6gZ4Y5gZ4 Genus p=6 |
 K5 / 4[gZ4Y5]3C Genus p=12 |
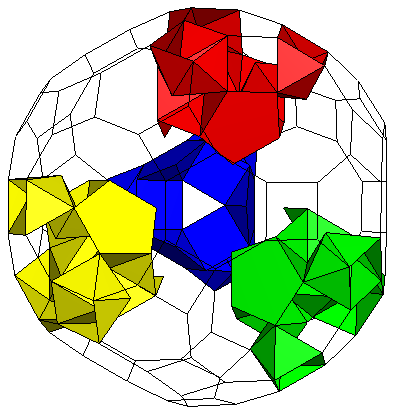
 K5 / [gZ4Y5gZ4Y5Y3A]5C Genus p=10. Y5 in yellow, Y5Y3A in green. |
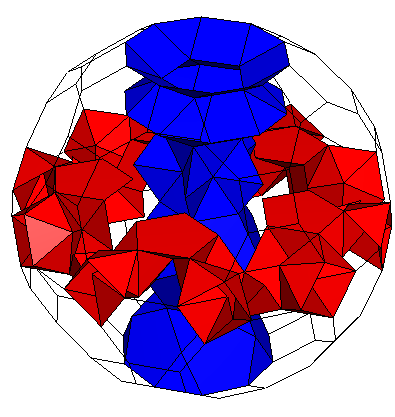 K5 / [gZ4Y5gZ4Y5Y3A]5C , S*. Genus p=11. Here S* contains a Stewart A5'' (link) |
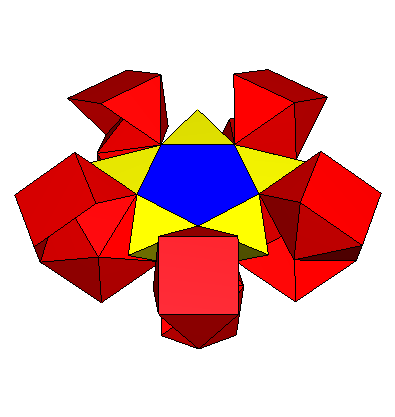 5gZ4(S5Y35A) |
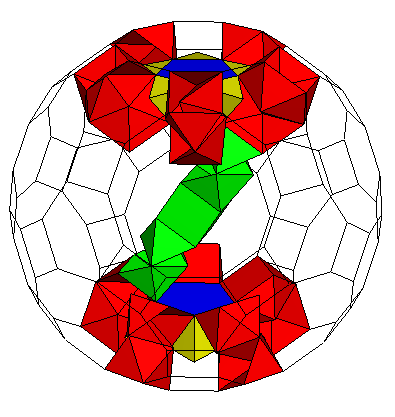 K5 / 2[5gZ4(S5Y35A)](Z4(P4)Z4). Genus p=9. |
 K5 / 2[5gZ4(S5Y35A)](Z4(P4)Z4) , [gZ4Y5gZ4Y5Y3A]5C. Genus p=19. |
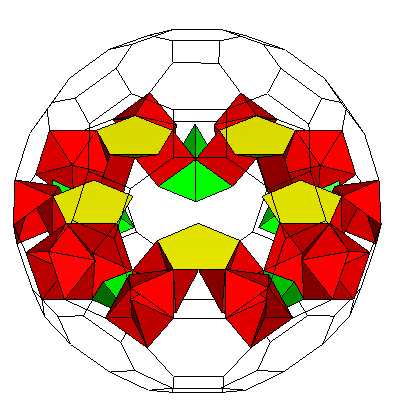
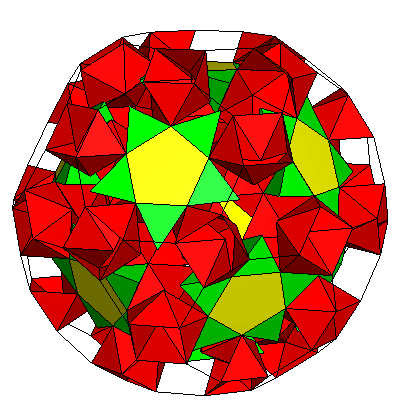 K5 / [30gZ420(S5Y35A)]C Genus p=48. Z4 in red, S5 in yellow, Y3A in green |
 K5 / [30gZ420(S5Y35A)]C(6Z4(P4)) Genus p=53. Colours as above plus 6Z4(P4) in orange. |