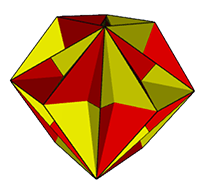
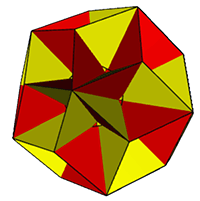
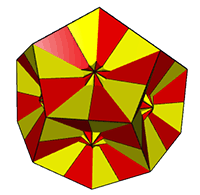
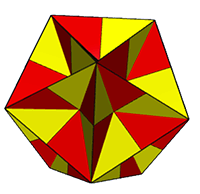
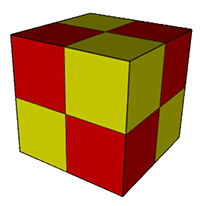
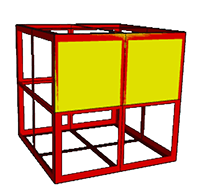
Rectangular Faced
Isohedral Polyhedra

An
isohedral
polyhedra is one which is transitive on all faces.
Between 1998 and 2001 Coxeter and Grunbaum ([1]
and [2])
described four isohedral polyhedra where the faces are
rectangular. One of these had previously appeared in Bruckner
1900 [3] (see above), which he had found while
exploring the duals to the stellations of the cuboctahedron.
Each of the rectangular isohedra can be created
from the dual of a
quasiregular
polyhedron by replacing each pair of parallel rhombi with
a ‘tube’ of four rectangles.
In 2026
Benjamin Klein developed a new
generating
method (personal correspondence January 2026). Each of the known
rectangular polyhedra contain two
sets of
'tubes'. In addition to the sets of tubes forming the thombic
faces used by Coxeter and Grunbaum above, the other set of tubes
(using the other two edges of the rectangles) form a
regular polygonal face. There is though no
mirror
symmetry between the top and bottom edges of these tubes. If
these
virtual faces are completed then they form two distinct polyhedra, each
with parallel faces and a common centre. The rectangular faces
can then be thought of as 'bridges' between the
parallel edges of these 'seed' polyhedra.
The rectangles can be
difficult to see in the completed polyhedron,
particularly in the more complex examples, so links
are provided below to each polyhedron with (a) one face
hightlighted, (b) a 'tube' of four rectangular faces highlighted (as
in the above example of the rectangulated rhombic triacontahedron), (c)
an example with both a rhombic and polygonal tube highlighted, (d) the
two seed polyhedra, and (e) the seed polyhedra with one polygonal tube
highlighted.
Klein then realised
that the rhombic triacontahedron and great rhombic triacontahedron
could also be used as seeds. As they both contain pairs of
parallel and aligned faces, bridging between them creates two new
forms, a 'small' case where the outer rhombic triacontahedron is linked
to
the near parallel face of the great rhombic triacontahedron (seeds with
1loop), and a 'large' case where it is linked to the far parallel face
(seeds with 1
loop). In both cases
the rectangular form has 60 faces which lie in coplanar pairs.
They do not share edges or vertices so are not degenerate. In the
small case, the parallel faces are distinct. In the large case
they
overlap. The polygonal tubes in both cases are semi-regular
decagons. Unfortunately the external appearance of both cases is
identical to that of the already known rectangular rhombic
triacontahedron. Displaying the inner edges though shows them to
be distinct examples of rectangular polyhedra.
The semi-regular
decagonal faces form edge-transitive polyhedra which are unfortunately
externally similar to the small and great stellated dodecahedra.
Names for these are taken from isotoxals.github.io/
where they can also be found under I53a_4, I53b_2,
I53a_1, and I53c_1.
One final simple
case exists if we regard the
square faces of the cube as being
'rectangular'. This then means
there
are now seven known isohedral rectangular polyhedra.
Coplanar Cases
Each of the Coxeter/Grunbaum
rectangular polyhedra has a mirror plane passing through the centre of
each rectangle. This implies that each rectangle can be
subdivided into two coplanar rectangles sharing an edge and remain
isohedral. This is mentioned briefly in by Coxeter and Grunbaum
in [2] These are presented in the table below.
The
faces are coloured red and yellow only to aid identification of the
individual faces. The Klein rectangular
polyhedra have no such mirror plane and so do not have coplanar
equivalents.
Two
further coplanar cases exist. Both are based on the frequency-2
cube and have 24 faces in coplanar sets of 4. One has all the
individual square faces, the second has overlapping 2 by 1
rectangles, this is mentioned by Grunbaum [2]. Again the faces are coloured
only to aid identification of the individual faces.
Further
Resources
A Zip
file containing all of the polyhedra referenced on this page is HERE. This contains
OFF, VRML (*.wrl) and HEDRON input files (*.txt).
Credits
Thank-you
to
Benjamin
Klein
for
sharing
his
discoveries
with
me
and
for
allowing
me
to
publish
them
here.
This
page
was
made
possible
using
Robert
Webb's
excellent
Great
Stella
program
(www.software3d.com).
Thanks
are
due
to
Roger
Kaufman
for
his VRML2OFF
utility,
and
to
Scott
Vorthmann
for
his VRML
Revival project.
All
VRML
files
were
generated
using Great
Stella and
post-processed
with VRML2OFF and HEDRON.
References
1. H.S.M.
Coxeter
and
B.Grunbaum
, “Face-Transitive
Polyhedra with Rectangular
Faces” C.R. Math. Rep. Aced. Sci.
Canada 20, 16-21, 1998 retrieved from https://www.math.ucdavis.edu/~deloera/MISC/LA-BIBLIO/trunk/Grunbaum2.pdf on 01/09/2025.
2. H.S.M.
Coxeter
and
B.Grunbaum
, “Face-Transitive
Polyhedra with Rectangular
Faces and Icosahedral Symmetry”
Discrete Comput Geom 25: 163-172, 2001 retrieved from https://link.springer.com/content/pdf/10.1007/s004540010087.pdf on 01/09/2025.
3. M. Brückner. "Vielecke und Vielflache:
Theorie und Geschichte". Teubner, Leipzig, 1900. Image retrieved
from https://bulatov.org/polyhedra/bruckner1900/index.html
on 16/09/2025
Back
to Rectangular and
Crossed-Rectaingular Faced
Isohedral Polyhedra
Back
to index