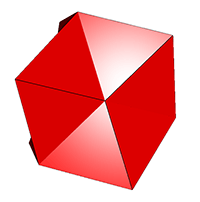
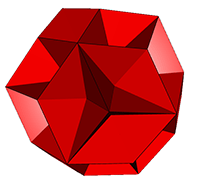
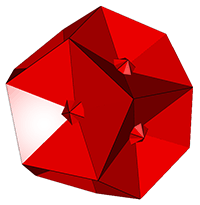
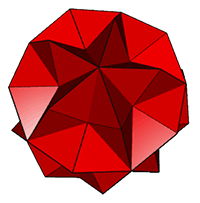
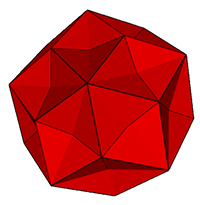
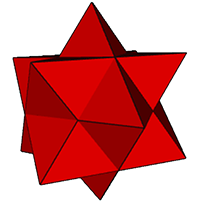
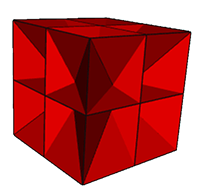
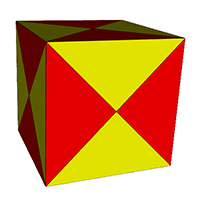
Crossed-Rectangular
Faced
Polyhedra
An
extension of the isohedral rectangular faced polyhedra would be to
consider isohedral polyhedra with
‘crossed
rectangular’ faces. Such a face retains two parallel edges of the
containing
rectangle, with the other two edges being replaced by the diagonals of
said
rectangle. I first wrote here about these in September 2025. To
my knowledge these have not been researched
previously.
A significant update was performed in January 2026 following
correspondence from Benjamin Klein,
who discovered a number of further
examples and also provided a methodology for their categorisation. A
total of 22 examples have now been generated between us.
Each crossed
rectangular faced isohedron (or 'XR') can be uniquely described by considering the
two virtual edges of the rectangle that is formed by the four vertices
of each face. These virtual edges fall into two sets. For
the XR to be isohedral, each set of virtual edges must be edges of an
edge-transitive polyhedron. This restricts consideration to the
regular polyhedra (the Platonics plus the Kepler-Poinsott's), quasiregular
polyhedra
(where distinct two polygons alternate around each vertex), and their
duals. The crossed rectangular faces themselves then form a
'bridge' between these two polyhedra (which we term the 'seeds').
I term
this 'Klein's bridge method'.
The examples fall into five categories.
Type I. Facetings obtained by
bridging across the rhombic isohedra (4 examples)
Type II.
Facetings obtained by
bridging across two regular
polyhedra (4 examples)
Type III. Facetings obtained by bridging between a regular
and a
quasiregular
polyhedron. (9 examples)
Type IV.
Facetings
obtained
by
bridging
between
two
quasiregular
polyhedra.
(3
examples)
Type V. Facetings obtained by bridging between
a
regular polyhedron and a degenerate set of faces (2 examples)
Consideration is then given to examples of crossed rectangular
polyhedra with coplanar faces
Both Klein and myself have conducted systematic searches of the
possibile combinations for types I to IV above and both feel that the
list for these types is complete. We cannot rule out however
further examples being found for type V, or cases where one of the
seeds is a compound of polyhedra.
Type I Bridge
facetings across a rhombic polyhedron
Using Great
Stella, I was in 2025 able to examine the facetings of the
Coxeter/Grunbaum isohedral rectangular polyhedra by replacing the
rectangular faces with crossed rectangles. New
polyhedra can be obtained by faceting the faces of the
rectangular
polyhedra with each rectangular polyhedron giving rise to two
crossed-rectangular
polyhedra. Using Klein's bridge method
these can be separated into two groups depending on whether the
rectangular
edges of the crossed rectangles are the edges which span acrosss the
rhombic polyhedra,
or whether they are the edges that form the rhombic faces
themselves. The first group is
described here. The second group is Type II below.
In the case
of the rhombic triacontahedron and
the great rhombic triacontahedron,
further cases can be generated by faceting.
The faces of these are unrelated to the
rectangular polyhedra or to each other.
These are
included under Type III below. Neither the Klein rectangular polyhedra nor the
duals of the ditrigonals yield any further cases
Again the crossed-rectangles can be
difficult to see in the completed polyhedron, so links
are provided below to each polyhedron with various faces
hightlighted. The crossed rectangles do not form the 'tubes' as
in the rectangular polyhedra, but do form 'loops' involving the
parallel edges of the crossed rectangles. For the diagonal
faces, they also form what I term 'rings' of faces with a common
centre.
For brevity, the term 'Crossed Rectangular' is
shortened to 'XR' in the table below. Bowers acronyms are used in
their names.
Type
II
Bridge
facetings
between two regular
polyhedra
The rhombic polyhedra
used in Type I above can also be faceted using the rectangular
edges of the crossed rectangles which are the edges that form the
rhombic faces to form what I term the 'crossed rectangular
compliment' of the above polyhedra. Using
Klein's
bridge
method,
these
can
now
be
described
as bridge polyhedra
between two regular seed polyhedra.
Notes
on
the
XR oct-tet:
1. Generating this
polyhedron from the rhombic dodecahedron results in a
compound of two identical tetrahedral polyhedra, one of which is imaged
in the table above.
2. This polyhedron could also be classed as a Type III as only
four faces of the octahedron are connected to the tetrahedron.
With tetrahedral symmetry, the octahedron could be regarded as a
quasiregular tetratetrahedron with two distinct sets of 4 faces.
Type
III
Bridge
facetings
between
a
regular
and
quasiregular
polyhedron
Klein also extended
his bridge method to produce new examples
of the isohedral crossed rectangular
polyhedra. Klein's method involves two polyhedra with a common
centre and with faces aligned. The first polyhedron,
which I term the 'seed' (cyan in the examples below), is a regular
polyhedron, one of the Platonic
or Kepler Poinsot polyhedra. The second
polyhedron, which in this instance I term the 'shell', is a
quasiregular polyhedron
containing one set of polygons (green
in the examples below) equivalent to those in the first polyhedron.
A systematic check
was made of the possibilities: one tetrahedral, two octahedral and
twelve icosahedral. Nine additional crossed rectangular polyhedra
were obtained, one octahedral and eight icosahedral. Where the
shell is a ditrigonal polyhedron, there is always a choice as to which
is
used as each set of n-gons is in the same position in all three
polyhedra. A new naming convention is used here, where 3dit means
either of the ditrigonal polyhedra containing triangles, 5dit means either of
the ditrigonal polyhedra containing pentagons and 5/2dit means either of
the ditrigonal polyhedra containing pentagrams. (The seed-shell models
show one of the two ditrigonals.)
Type
IV
Bridge
facetings
between
a two quasiregular
polyhedra
A systematic search was made
where both 'seed' and 'shell' polyhedra were quasiregular. In
this
case the distinction between the two becomes arbitrary so I refer to
both as shells. In addition to the octahedral case below, there
are
nine distinct icosahedal possibiliities in total, of which two resulted
in crossed
rectangular polyhedra.
Type V Bridge
facetings
between
a regular
polyhedron and a degenerate polyhedron.
Two octahedral
outliers were
also discovered by Klein which do not fit any of the above
categories.
Notes on the XR cube2-3os2
1. The shells are a
frequency-2 cube, and three frequency-2 orthogonal squares. The
central point of the cube and the squares is not included.
2. This polyhedron has two edge connected
faces per plane, and may be considered by some to be somewhat
degenerate.
3. The two colour model above is included for clarity only and
does not signify a difference between the faces.
Crossed
Rectangular
Polyhedra
with
coplanar
faces
Two further examples
can be obtained if coplanar faces sharing an edge are permitted.
One stems from the the
cube, with crossed-squares lie in coplanar pairs. Each
square
of
the
cube
is
replaced
by
two
complimentary
crossed-squares.
The second stems from
the the frequency-2 cube,
with crossed-squares lie in coplanar sets of eight.
In the images and links below, half
of the
crossed-squares have been highlighted for clarity
|
XR cube
|

XR
Frequency 2 cube
|
It is interesting to note that the XR cube
above is isohedral and isogonal and so could be regarded as a
degenerate noble
polyhedron.
Further
Resources
A Zip
file containing all of the polyhedra referenced on this page is HERE. This contains
OFF, VRML (*.wrl) and HEDRON input files (*.txt).
Credits
Thank-you
to
Benjamin
Klein
for
sharing
his
discoveries
with
me
and
for
allowing
me
to
publish
them
here.
Klein
discovered
the
majority
of
the
Type
III, IV and V polyhedra above.
This
page
was
made
possible
using
Robert
Webb's
excellent
Great
Stella
program
(www.software3d.com).
Thanks
are
due
to
Roger
Kaufman
for
his VRML2OFF
utility,
and
to
Scott
Vorthmann
for
his VRML
Revival project.
All
VRML
files
were
generated
using Great
Stella and
post-processed
with VRML2OFF and HEDRON.
Back to
Rectangular and Crossed-Rectangular
Faced
Polyhedra
Back
to index